3.1. Производная по направлению

Пусть отрезок длины направлен по вектору

, ,

Тогда его проекция на оси координат будет:

, , .

Если существует предел отношения , то он называется Производной функции в точке По направлению и обозначается символом , т. е.

или .

Теорема. Если функция дифференцируема в точке , то она имеет в этой точке производную по любому направлению , причем

.

Доказательство. Функция дифференцируема, поэтому

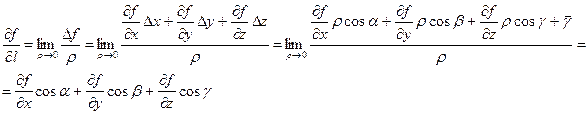
(т. к. , , и ).

В частности, если , то и .

Аналогично при , и при .

В случае функции двух переменных вектор будет лежать в плоскости , поэтому формула для производной по направлению будет иметь следующий вид:

.

Так как в плоскости , , то справедлива также формула

.

Если частные производные и представляют собой скорость изменения функции вдоль соответствующей оси координат, то Производная по направлению выражает скорость изменения функции по отношению к величине перемещения точки В направлении вектора .

В частности, если , то плоскость, проходящая через точку и вектор параллельно оси , пересечет поверхность по некоторой кривой . В этом случае скорость изменения функции в направлении вектора будет численно равна тангенсу угла , образованного касательной к кривой в точке , соответствующей точке , и вектором . При она будет выражать крутизну возрастания функции в направлении вектора , а при - крутизну убывания.

Таким образом, производная по направлению оказывается весьма полезной при исследовании поведения функции в окрестности заданной точки.

Пример 15. Найти производную функции в точке по направлению от точки в точке .

Решение. Найдем вектор и соответствующий ему единичный вектор :

.

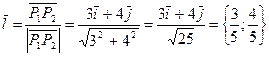Таким образом, вектор имеет следующие направляющие косинусы , .

Теперь найдем частные производные функции :

,

,

И их значения в точке :

,

.

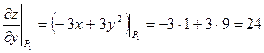Подставляя в формулу найденные значения частных производных и направляющих косинусов, получим искомую производную функции по направлению вектора :

.

< Предыдущая		Следующая >