2.9. Дифференциалы высших порядков

Дифференциалом -ого порядка функции называется дифференциал от дифференциала -ого порядка, как от функции независимых переменных и .

Таким образом, и рассматриваются при этом как величины, не зависящие от и .

Поэтому

Или, при условии непрерывности смешанных производных:

.

Аналогично

.

Рассмотрим сложную функцию , где , .

Тогда на основании теоремы об инвариантности формы первого дифференциала получим

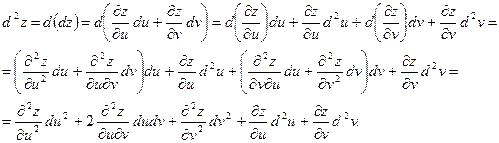
Таким образом, в случае, если аргументы и являются функциями независимых переменных, форма второго дифференциала изменяется на величину .

Это объясняется тем, что теперь, вообще говоря, и отличны от нуля. Если же и будут независимыми переменными, то и не будут зависеть от и , поэтому

.

Аналогично, , и мы получим уже известную форму второго дифференциала.

< Предыдущая		Следующая >