2.8. Частные производные высших порядков
Если функция ![]() имеет непрерывные частные производные
имеет непрерывные частные производные
![]() ,
, ![]() ,
,
То они снова являются функциями переменных ![]() и
и ![]() , и если эти функции дифференцируемы в точке
, и если эти функции дифференцируемы в точке ![]() , то от каждой из них можно снова находить частные производные по
, то от каждой из них можно снова находить частные производные по ![]() и
и ![]() . В результате получим вторые частные производные, которые обозначаются так:
. В результате получим вторые частные производные, которые обозначаются так:
![]() ;
;
![]() ;
;
 ;
;
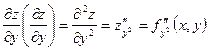 .
.
Производные ![]() и
и ![]() называются Смешанными – они получаются последовательным дифференцированием функции
называются Смешанными – они получаются последовательным дифференцированием функции ![]() сначала по
сначала по ![]() , затем по
, затем по ![]() или наоборот.
или наоборот.
Производные второго порядка можно снова дифференцировать, получим частные производные третьего порядка. Из будет уже восемь:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Вообще, частное производной ![]() -ого порядка называется частная производная от какой-либо частной производной
-ого порядка называется частная производная от какой-либо частной производной ![]() -ого порядка.
-ого порядка.
Например, ![]() есть производная
есть производная ![]() -ого порядка.
-ого порядка.
Здесь ![]() дифференцируется сначала
дифференцируется сначала ![]() Раз по
Раз по ![]() , потом
, потом ![]() - по
- по ![]() . Для функций большего числа переменных частные производные высшиш порядков определяются аналогично.
. Для функций большего числа переменных частные производные высшиш порядков определяются аналогично.
Пример 12. ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Замечаем, что результат дифференцирования в подчеркнутых производных не зависит от порядка, в котором происходит это дифференцирование. И это не случайно, о чем говорит следующая теорема.
Теорема. Если функция ![]() и ее частные производные
и ее частные производные ![]() ,
, ![]() ,
, ![]() и
и ![]() определены и непрерывны в точке
определены и непрерывны в точке ![]() и в некоторой ее окрестности, то в этой точке вторые смешанные производные равны между собой, т. е.
и в некоторой ее окрестности, то в этой точке вторые смешанные производные равны между собой, т. е.
|
|
(10) |
Следствие. При непрерывности соответствующих частных производные результат повторного дифференцирования функции двух независимых переменных не зависит от порядка дифференцирования.
Например, ![]() .
.
Пример 13. Дана функция ![]() .
.
Найти частные производные первого и второго порядка. Убедиться, что смешанные производные равны.
![]() - производная по
- производная по ![]() найдена в предположении, что
найдена в предположении, что ![]() - постоянная величина в момент дифференцирования.
- постоянная величина в момент дифференцирования.
![]() - производная по
- производная по ![]() найдена в предположении, что
найдена в предположении, что ![]() - постоянная величина.
- постоянная величина.
![]() ,
, ![]() ,
,
 . Действительно,
. Действительно, ![]() .
.
Пример 14. Проверить, что функция ![]() удовлетворяет уравнению
удовлетворяет уравнению ![]() .
.
Решение.
![]() (
(![]() ,
, ![]() - постоянные),
- постоянные),
![]() (
(![]() ,
,![]() - постоянные),
- постоянные),
![]() (
(![]() ,
,![]() - постоянные).
- постоянные).
Суммируем найденные производные:
 ,
,
Что и требовалось доказать.
| < Предыдущая | Следующая > |
|---|