2.7. Инвариантность формы первого дифференциала

В том случае, когда и являются независимыми аргументами функции , была установлена следующая форма ее дифференциала:

.

(9)

В случае, если зависим от и сложным образом, т. е. через посредство некоторых функций и или , то частные производные, входящие в выражение (9), будут выражаться по формулам (2):

,

.

При этом оказывается, что форма дифференциала (9) не изменится, если мы его выразим только через и и их дифференциалы, т. к. имеет место теорема об инвариантности формы первого дифференциала функции многих переменных:

Теорема. Дифференциал функции сохраняет один и тот же вид независимо от того, являются ли ее аргументы и Независимыми переменными или функциями от независимых переменных.

Доказательство. В случае независимых переменных и по теореме 2 п. 2.3:

.

Если же и , то, подставляя и из (2) в (9) после группировки выражений, содержащих и , получим

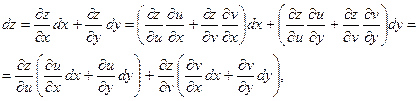
И так как здесь в скобках стоят полные дифференциалы от и , то окончательно получим

.

Замечание. Как и в случае функции одной переменной, для дифференциалов более высокого порядка, о которых речь будет ниже, эта теорема не верна – их величина и форма в случае независимых переменных и отлична от величины и формы в случае, если и будут функциями других независимых переменных.

< Предыдущая		Следующая >