2.5. Производная сложной функции
Пусть ![]() , причем
, причем ![]() ,
, ![]() , т. е.
, т. е. ![]() зависит от
зависит от ![]() и
и ![]() через посредство двух других функций
через посредство двух других функций ![]() и
и ![]() .
.
В этом случае функция ![]() называется Сложной функцией переменных
называется Сложной функцией переменных ![]() и
и ![]() . Подставляя
. Подставляя ![]() и
и ![]() в выражение для
в выражение для ![]() , получим непосредственную зависимость
, получим непосредственную зависимость ![]() от переменных
от переменных ![]() и
и ![]()
|
|
(1) |
Однако и в теории, и в приложениях важно уметь находить частные производные ![]() и
и ![]() , не пользуясь равенством (1).
, не пользуясь равенством (1).
Теорема. Если функции ![]() и
и ![]() дифференцируемы в точке
дифференцируемы в точке ![]() , а функция
, а функция ![]() дифференцируема в соответствующей точке
дифференцируема в соответствующей точке ![]() , то сложная функция
, то сложная функция ![]() дифференцируема в точке
дифференцируема в точке ![]() , причем
, причем
|
|
(2) |
Формулы (2) обобщаются на случай любого числа независимых переменных. В частности, если ![]() и
и ![]() , то функция
, то функция ![]() будет сложной функцией одной переменной
будет сложной функцией одной переменной ![]() и ее полная производная по этой переменной будет
и ее полная производная по этой переменной будет
|
|
(3) |
Если здесь положить ![]() , т. е.
, т. е. ![]() , то получим
, то получим
|
|
(4) |
Пример 10.
1. ![]() ,
, ![]() ,
, ![]() . Найти
. Найти ![]() и
и ![]() .
.
По формуле (2) имеем
![]() ,
,
![]() .
.
2. ![]() . Найти
. Найти ![]() .
.
Пусть ![]() ,
, ![]() . Тогда
. Тогда ![]() .
.
По формуле (2) имеем ![]() .
.
3. ![]() ,
, ![]() ,
, ![]() . Найти
. Найти ![]() .
.
По формуле (2) имеем
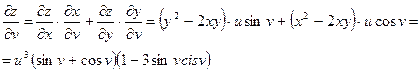
4. ![]() ,
, ![]() ,
, ![]() . Найти
. Найти ![]() .
.
По формуле (3) имеем
![]() .
.
5. ![]() . Найти
. Найти ![]() .
.
![]() , где
, где ![]() ,
, ![]() .
.
6. ![]() ,
, ![]() . Найти
. Найти ![]() .
.
По формуле (4) имеем
![]() .
.
| < Предыдущая | Следующая > |
|---|
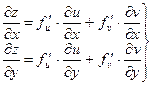 .
.