2.4. Приложение полного дифференциала

Ограничиваясь дифференциалом функции как главной части приращения, получим приближенное равенство , полезное в приближенных вычислениях. В развернутой форме оно будет:

Или

.

Для вычисления значения функции в некоторой точке записывают , в виде суммы , , стараясь подобрать , возможно меньшими, но так, чтобы в полученной точке легко вычислялись значения функции и ее производных.

Пример 9. Дана функция и две точки , .

Требуется: 1) Вычислить значения в точке ;

2) Вычислить приближенное значение функции в точке , исходя из значения функции в точке , заменяя приращение функции при переходе от точки к точке дифференциалом;

3) Оценить в процентах относительную погрешность, получающуюся при замене приращения функции ее дифференциалом.

Решение.

По условию , , следовательно

; ; ; ;

; .

Тогда 1) .

2) ,

,

,

, ,

, .

Тогда

.

3)относительная погрешность вычисляется по формуле

.

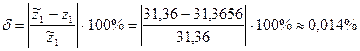< Предыдущая		Следующая >