07. Производные и дифференциалы высших порядков

1°. Если первые частные производные функции в свою очередь являются дифференцируемыми функциями, то можно определить частные производные II порядка:

;

;

;

.

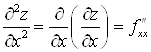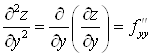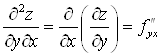Аналогично определяются производные более высоких порядков.

2. Частные производные

и

называются смешанными. В тех точках, где смешанные производные непрерывны, они равны. Это утверждение справедливо и для производных более высоких порядков:

.

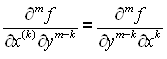3°. В пространстве Rn смешанные производные раз дифференцируемой функции равны, если они непрерывны.

.

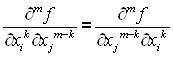Примеры.

А) Проверить, что смешанные производные II порядка для функции равны.

Б) Доказать, что функция удовлетворяет уравнению Лапласа:

.

Решение:

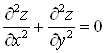А) Вычислим сначала первые производные функции :

;

;

;

.

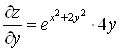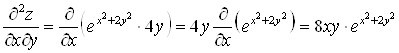Очевидно, что .

Б) ;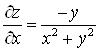

;

;

;

.

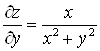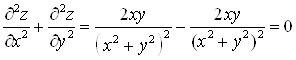4°. Пусть функция F(X1, X2, ... Xn) — дифференцируема в т. (X1 ... Xn), тогда

.

Если — дифференцируемы, то может быть определен дифференциал II порядка

Аналогично определяются дифференциалы более высоких порядков:

.

5°. Если X1, X2, ... Xn — независимые переменные, то второй дифференциал представляет собой квадратичную форму относительно :

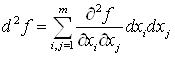
Или в операторном виде:

.

6°. Для функции двух переменных в случае, если — независимые переменные, имеет вид:

.

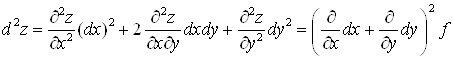7°. Второй дифференциал и все последующие не обладают свойством инвариантности формы: если — функции других переменных то

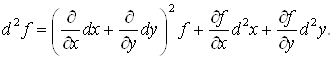
Примеры:

А) Найти если

Б) Найти если , где

В) Найти если

Решение:

А) Поскольку независимые переменные, то

.

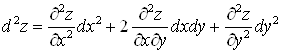Вычислим производные

; ;

;

;

;

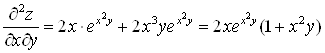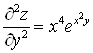Б) Функция , — сложная

,

; ;

; ; ,

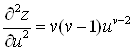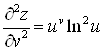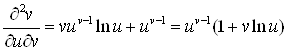В) Данная функция зависит от трех свободных переменных

;

;

; ; ;

; ; .

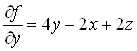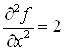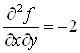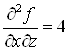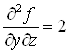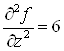Все вторые производные второго порядка не зависят от точки.

8°. Пусть функция задана неявно уравнением .

Тогда ; .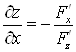

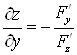При вычислении вторых производных следует учитывать, что первые производные зависят от и непосредственно и через .

Пример: Найти и , если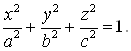

Решение:

Функция задана неявно уравнением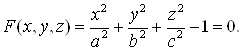

,

,

,

,

,

.

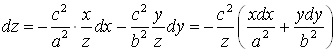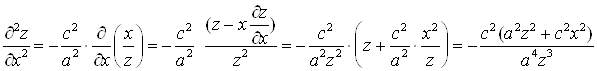
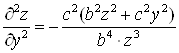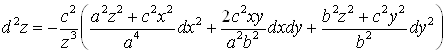< Предыдущая		Следующая >