02. Пространство Rn. Множества в Rn

1°. Пространством Rn Называют множество упорядоченных наборов вещественных чисел (X1, X2, ... Xn).

Каждый такой набор называют точкой в Rn и обозначают одной буквой X, а числа Xi — координатами точки.

2°. Расстоянием между двумя точками X(1), X(2) в пространстве Rn называют число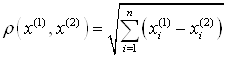

В частности в

В

3°. Шаром радиуса e с центром в т. A Î Rn называют множество

Это множество в Rn называют e-окрестностью точки A.

В представляет собой

В — внутренность круга радиуса с центром в точке а:

,

В — внутренность шара радиуса с центром в точке а:

,

4°. Точка X Î Rn называется внутренней точкой множества G Ì Rn, если она принадлежит этому множеству вместе с какой-либо e-окрестностью (т. е. шаром ).

5°. Множество, состоящее только из внутренних точек, называется открытым.

6°. Точка X Î Rn называется внешней для множества G Ì Rn, если она является внутренней для .

7°. Точка X Î Rn называется граничной для множества G, если она не является ни внутренней точкой этого множества, ни внешней.

8°. Множество называется замкнутым, если оно содержит все свои граничные точки.

9°. Диаметром множество G Ì Rn называют величину

10°. Множество называется ограниченным, если его диаметр конечен.

11°. Множество называется связным, если любые 2 его точки можно соединить кривой, принадлежащей множеству.

< Предыдущая		Следующая >