03. Функции в Rn. Предел функции
1°. Пусть G — множество в Rn. Если для любого X Î G по некоторому закону поставлено в соответствие вещественное число Y, то говорят, что на множестве G определена функция Y = F(X).
Множество G называется множеством определения функции F(X).
2°. В пространстве R2 аргументы функций обычно обозначают X и Y, а функцию Z (Z = F(X, y)). Областью определения в этом случае является множество в плоскости 
.
3°. Геометрически уравнение Z = F(X, y) задает поверхность. Линии, во всех точках которой функция F(X, y) принимает одно и то же значение называют линиями уровня. Они задаются уравнениями F(X, y) = C.
Примеры решения задач. Найти и изобразить множество определения функции. Является ли это множество открытым (замкнутым), ограниченным (неограниченным), связным (несвязным)?
А) 
Б) 
А) Логарифмическая функция определена в тех точках, где аргумент строго положителен, т. е. при 
Парабола 
делит плоскость на 2 части — внутреннюю и внешнюю. Неравенству 
удовлетворяет внешняя часть. Граница в множество определения не входит. Значит, множество открыто. Очевидно, диаметр множества бесконечен, т. к. множество содержит точки, отстоящие друг от друга как угодно далеко. Значит, множество определения неограниченно. Это множество связно: любые две точки можно соединить кривой, принадлежащей множеству.
Б) Функция 
Определена там, где 
Это неравенство выполняется если 
, 
,
,
.
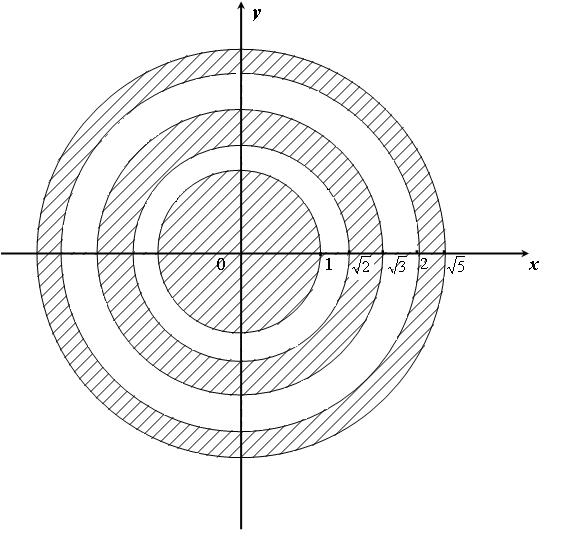
Первое неравенство выполняется внутри и на границе круга единичного радиуса, второе — в кольце между окружностями радиусов 
и 
, и т. д.
Область определения является замкнутым, неограниченным множеством. Оно не является связным, т. к. две точки из разных колец нельзя соединить кривой, полностью принадлежащей множеству.
4°. Число A называется пределом функции двух переменных при 
, если 
: 
:
Обозначение: 
.
Наличие предела 
при равного A говорит о том, что при стремлении по любому пути значение 
.
Из наличия последовательных пределов 
и 
не следует существование 
, даже если последовательные пределы равны.
Примеры.
Вычислите предел или докажите, что он не существует:
А)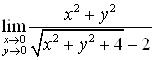 
,
Б) 
.
А) 
.
Б) Покажем, что предел б) не существует. Пусть т. 
вдоль прямой 
,
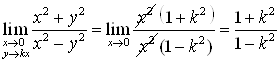из чего следует, что на различных прямых предельные значения функции различны, а, значит, предел не существует.
5°. Функция , определенная в т. 
и в некоторой ее окрестности называется непрерывной в т. , если 
.
6°. Функция, непрерывная в каждой точке некоторого множества, называется непрерывной на этом множестве.
7°. Если функция непрерывна на ограниченном замкнутом множестве 
, то она обладает следующими свойствами:
— она ограничена на этом множестве;
— принимает на этом множестве наибольшее и наименьшее значение.
8°. Пусть 
— приращение, которое получает функция , если переменная X получает приращение DX, а Y не изменяется. Предел 
(если он существует) называют частной производной функции по переменной X и обозначают 
или 
;
,
.
Аналогично определяются первые производные функции любого числа переменных. Вычисляют частные производные по тем же правилам, что производные функции одной переменной, при условии, что остальные переменные фиксируются.
Примеры:
Вычислить частные производные функций а) 
Б)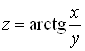 
,
В) 
.
А) 
,
.
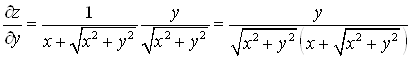Б) 
,
.
В) Функция зависит от трех переменных и имеет три первые частные производные:
,
,
.
| < Предыдущая | Следующая > |
|---|
