08.4. Решение типовых примеров
1 Исследовать функцию ![]() и построить ее график.
и построить ее график.
Решение. 1) находим ![]() , определяем точки разрыва, нули, точки пересечения графика функции с осью
, определяем точки разрыва, нули, точки пересечения графика функции с осью ![]() , периодичность, симметрию. Функция определена при тех значениях
, периодичность, симметрию. Функция определена при тех значениях ![]() , для которых, как следует из определения арксинуса, выполнено неравенство
, для которых, как следует из определения арксинуса, выполнено неравенство
![]() .
.
Данное неравенство равносильно неравенству ![]() , которое верно для любых вещественных
, которое верно для любых вещественных ![]() .
.
Итак, ![]()
![]() .
.
Функция ![]() непрерывна в любой точке (как частное двух непрерывных функций). Поэтому функция
непрерывна в любой точке (как частное двух непрерывных функций). Поэтому функция ![]() также непрерывна в любой точке (как суперпозиция непрерывных функций).
также непрерывна в любой точке (как суперпозиция непрерывных функций).
Функция непериодическая.
Поскольку
![]()
![]()
![]() =
=![]() ,
,
То функция является нечетной. Поэтому вместо всей области определения достаточно рассмотреть полупрямую ![]() .
.
При ![]() имеем
имеем ![]() . Других нулей функция не имеет. На полупрямой
. Других нулей функция не имеет. На полупрямой ![]() функция является положительной;
функция является положительной;
2) асимптоты графика функции. В силу непрерывности функции ![]() на
на ![]() , график функции не имеет вертикальных асимптот. Для нахождения наклонной асимптоты при
, график функции не имеет вертикальных асимптот. Для нахождения наклонной асимптоты при ![]() вычислим следующие пределы:
вычислим следующие пределы:
![]()
![]() =0,
=0,
![]()
![]()
![]() .
.
Отсюда следует, что прямая ![]() является горизонтальной асимптотой при
является горизонтальной асимптотой при ![]() .
.
Аналогично устанавливается, что прямая ![]() – горизонтальной асимптотой при
– горизонтальной асимптотой при ![]() ;
;
3) точки возможного экстремума и интервалы монотонности функции.
Найдем точки возможного экстремума на полупрямой ![]() . Вычислим производную функции при
. Вычислим производную функции при ![]() :
:

 .
.
Отсюда видно, что производная не обращается в нуль ни в одной точке. Так как ![]() ,
, ![]() , то точка
, то точка ![]() является точкой излома. Значит, имеем только одну точку возможного экстремума
является точкой излома. Значит, имеем только одну точку возможного экстремума ![]() .
.
Промежутки монотонности функции определяются знаком производной: ![]() при
при ![]() ,
, ![]() при
при ![]() .
.
Знак производной при переходе через точку ![]() меняется с плюса на минус. Поэтому в точке
меняется с плюса на минус. Поэтому в точке ![]() функция имеет локальный максимум, причем
функция имеет локальный максимум, причем ![]() .
.
Отметим, что в точке ![]() функция непрерывна, а ее производная имеет разрыв 1-го рода. Значит, точка графика
функция непрерывна, а ее производная имеет разрыв 1-го рода. Значит, точка графика ![]() является угловой точкой;
является угловой точкой;
4) промежутки выпуклости и вогнутости, точки перегиба. Вторая производная при ![]() имеет вид
имеет вид
![]() .
.
Направление выпуклости определяется знаком второй производной:
– ![]()
![]() при
при ![]() , значит график функции на этом промежутке выпуклый,
, значит график функции на этом промежутке выпуклый,
– ![]()
![]() при
при ![]() , значит график функции на этом промежутке вогнут.
, значит график функции на этом промежутке вогнут.
Так как вторая производная обращается в нуль лишь при ![]() и при переходе через точку
и при переходе через точку ![]() меняет знак, то в точке
меняет знак, то в точке ![]() график функций имеет перегиб.
график функций имеет перегиб.
Результаты исследования функции заносим в таблицу 8.2.
Таблица 8.2 – Результаты исследования функции ![]()
|
|
0 |
|
1 |
|
|
|
2 |
+ |
Не сущ. |
– |
|
|
0 |
– |
Не сущ. |
+ |
|
|
0 |
|
|
|
|
Точка Перег. |
Угл. точ. |
Исходя из результатов, содержащихся в таблице 8.2, строим график данной функции на полупрямой ![]() .
.
Используя нечетность функции, достраиваем ее график на всей области определения (рисунок 8.1).
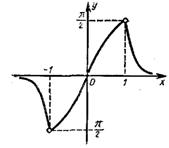
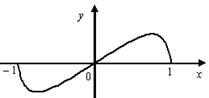
Рисунок 8.1 – График функции ![]()
2 Исследовать функцию, заданную параметрическими уравнениями, и построить график
![]() ,
, ![]() . (8.3)
. (8.3)
Решение. 1) функции ![]() ,
, ![]() определены на множестве
определены на множестве
![]() .
.
Поскольку
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
То ![]() – вертикальная асимптота кривой.
– вертикальная асимптота кривой.
Найдем односторонние пределы в точках ![]() и
и ![]() :
:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Отсюда следует, что при ![]() и
и ![]() возможны наклонные асимптоты.
возможны наклонные асимптоты.
Так как при ![]()
![]() ,
, ![]() ,
,
То прямая ![]() – наклонная асимптота.
– наклонная асимптота.
Так как при ![]()
![]() ,
, ![]() ,
,
То прямая ![]() – наклонная асимптота.
– наклонная асимптота.
Итак,
![]() ,
,
![]() ;
;
2) так как
![]() ,
, ![]() ,
,
То график функции симметричен относительно начала координат ![]() . Поэтому рассмотрим график функции только на множестве
. Поэтому рассмотрим график функции только на множестве ![]() ;
;
3) на множестве ![]() имеем
имеем ![]() при
при ![]() ,
, ![]() при
при ![]() и
и ![]() ;
;
4) найдем производные функций ![]() ,
, ![]() :
:
![]() ,
, ![]() .
.
На множестве ![]()
![]() и
и ![]() при
при
![]()
![]() 0,47 и
0,47 и ![]()
![]() 1,51.
1,51.
Тогда ![]() ,
, ![]() и
и ![]() ,
, ![]() , т. е. имеем точки возможного экстремума
, т. е. имеем точки возможного экстремума ![]() и
и ![]() ;
;
5) найдем производные ![]() и
и ![]() :
:
![]()
![]() ,
,  .
.
Отсюда ![]() при
при ![]() ,
, ![]() при
при ![]() ;
;
6) составим таблицу результатов исследования (таблица 8.3):
Таблица 8.3 – Результаты исследования функции
|
|
|
0,47 |
|
|
1,51 |
|
|
|
|
0,6 |
|
|
-0,7 |
|
|
|
|
0,3 |
|
|
2,3 |
|
|
Знак |
+ |
+ |
+ |
– |
– |
– |
7) строим часть кривой, соответствующую множеству ![]() . Далее, используя симметрию кривой, построим всю кривую (рисунок 8.2).
. Далее, используя симметрию кривой, построим всю кривую (рисунок 8.2).

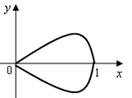
Рисунок 8.2 – График функции (8.3)
3 Исследовать функцию заданную параметрическими уравнениями и построить график
![]() ,
, ![]() . (8.4)
. (8.4)
Решение. 1) функции ![]() ,
, ![]() определены на
определены на ![]() .
.
При этом
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Таким образом, возможны наклонные асимптоты.
Так как
![]() ,
,
То наклонных асимптот нет;
2) свойствами симметрии и периодичности функция не обладает;
3) имеем ![]() при
при ![]() и
и ![]() ;
; ![]()
![]() при
при ![]() ,
, ![]() и
и ![]() ;
;
4) найдем производные функций ![]() ,
, ![]() :
:
![]() ,
, ![]() .
.
Имеем ![]() при
при ![]() ,
, ![]() при
при ![]() и
и ![]() . Тогда точки возможного экстремума
. Тогда точки возможного экстремума ![]() ,
, ![]() ;
;
5) найдем производные ![]() и
и![]() :
:
![]()
 ,
, ![]()
![]() ,
, ![]() .
.
Отсюда ![]() при
при ![]() ,
, ![]() при
при ![]() ;
;
6) составим таблицу результатов исследования (таблица 8.4);
Таблица 8.4 – Результаты исследования функции (8.4)
|
|
|
-1 |
|
1 |
|
|
|
|
-3 |
|
1 |
|
|
|
|
-2 |
|
2 |
|
|
Знак |
+ |
+ |
+ |
- |
7) строим график функции. Первая производная ![]() не определена в точке
не определена в точке ![]() , поэтому точка
, поэтому точка ![]() является угловой точкой графика.
является угловой точкой графика.
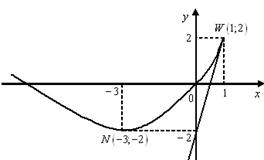
Рисунок 8.3 – График функции ![]() ,
, ![]()
4 Исследовать функцию, заданную неявно и построить ее график
![]() (8.5)
(8.5)
Решение. 1 способ. Разрешая данное уравнение относительно ![]() , получим
, получим ![]() .
.
Функции ![]() и
и ![]() симметричны относительно оси
симметричны относительно оси ![]() , то исследование можно провести для функции
, то исследование можно провести для функции ![]() . Эта функция определена на отрезке
. Эта функция определена на отрезке ![]() , т. е.
, т. е. ![]()
![]() . Функция
. Функция ![]() равна нулю при
равна нулю при ![]() ,
, ![]() ,
, ![]() . На области определения
. На области определения ![]() функция является нечетной.
функция является нечетной.
Находим производные функции ![]() :
:
![]() =
=![]() ,
, ![]() =
= .
.
Точками возможного экстремума являются точки:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Точки ![]() и
и ![]() являются граничными точками области определения
являются граничными точками области определения ![]() . Определим характер точек
. Определим характер точек ![]() и
и ![]() с помощью второй производной:
с помощью второй производной:
![]() =
=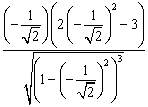 = 4 > 0,
= 4 > 0,
![]() =
=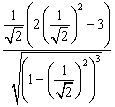 = – 4 < 0.
= – 4 < 0.
Следовательно, ![]() является точкой минимума,
является точкой минимума, ![]() – точкой максимума. Значения функции
– точкой максимума. Значения функции ![]() в этих точках соответственно равны:
в этих точках соответственно равны:
![]() =
= = –
= –![]() ,
,
![]() =
=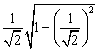 =
= ![]() .
.
В точке ![]() вторая производная обращается в нуль. При
вторая производная обращается в нуль. При ![]() имеем
имеем ![]() <0, при
<0, при ![]() имеем
имеем ![]() >0. Следовательно, точка
>0. Следовательно, точка ![]() является точкой перегиба графика функции
является точкой перегиба графика функции ![]() .
.
График функции ![]() изображен на рисунке 8.4. Отображая построенный график симметрично относительно оси
изображен на рисунке 8.4. Отображая построенный график симметрично относительно оси ![]() , получим график исходной функции
, получим график исходной функции ![]() (рисунок 8.5). Видно, в точке
(рисунок 8.5). Видно, в точке ![]() график пересекает себя, поэтому является точкой самопересечения.
график пересекает себя, поэтому является точкой самопересечения.
|
|
|
|
Рисунок 8.4 – График функции
|
Рисунок 8.5 – График функции
|
2 способ. Полагая ![]() из уравнения
из уравнения ![]() , получим
, получим ![]() . Отсюда
. Отсюда ![]() . Поскольку
. Поскольку ![]() , то график функции симметричен относительно оси
, то график функции симметричен относительно оси ![]() , и поэтому будем рассматривать случай
, и поэтому будем рассматривать случай ![]() .
.
Тогда параметрические уравнения кривой имеют вид:
![]() ,
, ![]() . (8.6)
. (8.6)
Исследование данной функции проводится по схеме для функций, заданных параметрическими уравнениями.
1) функции ![]() ,
, ![]() определены на
определены на ![]() .
.
При этом
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Таким образом, наклонные асимптоты отсутствуют;
2) так как
![]() ,
, ![]() ,
,
То график функции симметричен относительно оси ![]() .
.
Свойством периодичности функция не обладает;
3) имеем ![]() ,
, ![]() при
при ![]() ;
;
4) найдем производные функций ![]() ,
, ![]() :
:
![]() ,
, ![]() .
.
Имеем ![]() при
при ![]() ,
, ![]() в точках
в точках ![]() и
и ![]() ;
;
5) найдем производные ![]() и
и ![]() :
:
![]()
![]() ,
, ![]()
![]() .
.
Так как ![]() , то
, то ![]() . Тогда
. Тогда
![]() ,
, ![]() .
.
Так как ![]() , то
, то ![]() . Тогда
. Тогда
![]() ,
, ![]() ;
;
6) строим график функции, заданной уравнениями (8.6). Отображая симметрично относительно оси ![]() , получаем график исходной функции (рисунок 8.7).
, получаем график исходной функции (рисунок 8.7).
|
|
|
|
Рисунок 8.6 – График функции
|
Рисунок 8.7 – График функции
|
5 Исследовать и построить график функции
![]() . (8.7)
. (8.7)
Решение. Данная функция при тех значениях ![]() , для которых, как следует из определения полярного радиуса, выполнено неравенство
, для которых, как следует из определения полярного радиуса, выполнено неравенство
![]() .
.
Кроме того, функция ![]() является
является ![]() Периодической, то достаточно рассмотреть промежуток
Периодической, то достаточно рассмотреть промежуток
![]() .
.
Поскольку
![]() ,
,
![]() ,
,
То прямая
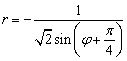
Является асимптотой при ![]() .
.
Аналогично
![]() ,
,
![]() ,
,
И прямая

Является асимптотой при ![]() .
.
Так как ![]() , то это одна и та же прямая.
, то это одна и та же прямая.
Если ![]() , то из уравнения (8.7) следует
, то из уравнения (8.7) следует ![]() =0, т. е. имеем точку
=0, т. е. имеем точку ![]() .
.
При ![]() , полагая
, полагая ![]() , получим параметрическое задание кривой:
, получим параметрическое задание кривой:
![]() ,
, ![]() . (8.8)
. (8.8)
Найдем производные
 ,
,  .
.
Имеем ![]() при
при ![]() ,
, ![]() при
при ![]() и
и ![]() .
.
Найдем производные ![]() и
и ![]() :
:
![]() ,
,  .
.
При ![]() имеем
имеем ![]() <0 и
<0 и ![]() , значит функция убывает и вогнута, следовательно, подходит к асимптоте сверху.
, значит функция убывает и вогнута, следовательно, подходит к асимптоте сверху.
При ![]() имеем
имеем ![]() и
и ![]() , значит, функция убывает и вогнута. При этом
, значит, функция убывает и вогнута. При этом
![]()
При ![]() имеем
имеем ![]() и
и ![]() , значит, функция возрастает и вогнута. При этом
, значит, функция возрастает и вогнута. При этом
![]() ,
, ![]() .
.
При ![]() имеем
имеем ![]() и
и ![]() , значит, функция возрастает и выпукла. При этом
, значит, функция возрастает и выпукла. При этом
![]() ,
, ![]() .
.
При ![]() имеем
имеем ![]() и
и ![]() , значит, функция возрастает и выпукла.
, значит, функция возрастает и выпукла.
Так как ![]() , то
, то ![]() является точкой возврата.
является точкой возврата.
График функции (8.7) называется Декартов лист и изображен на рисунке 8.8. В декартовой системе координат декартов лист задается уравнением:
![]() .
.
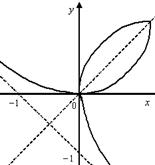
Рисунок 8.8. Декартов лист
| < Предыдущая | Следующая > |
|---|