07.5. Решение типовых примеров

1 Найти промежутки выпуклости и вогнутости графика функции .

Если , то и кривая выпукла.

Если , то и кривая вогнута.

Итак, кривая выпукла на промежутке , вогнута на промежутке .

2 Найти точки перегиба графика функции:

А); б).

Решение. а) первая и вторая производные равны соответственно

Так как в точке , то исследуем эту точку на перегиб. В окрестности точки при , то и кривая выпукла, при , то и кривая вогнута. Следовательно, – точка перегиба, при этом –2.

Б) имеем:

, .

Вторая производная не обращается в нуль ни при каких значениях и не существует в точке . В окрестности точки получим при , то и кривая выпукла, при , то и кривая вогнута. Следовательно, – точка перегиба, при этом 2.

3 Найти асимптоты графика функции .

Решение. 1) функция определена на промежутках

Так как

, ,

То прямая является вертикальной асимптотой.

2) наклонные асимптоты:

Следовательно, наклонная асимптота имеет вид

3) горизонтальных асимптот нет, так как

4 Исследовать функцию и построить ее график.

Решение. Для построения графика функции проведем ее исследование по приведенной схеме.

1) находим , определяем точки разрыва, нули, точки пересечения графика функции с осью , периодичность, симметрию. Функция неопределенна в точках, где знаменатель обращается в нуль, т. е. при , . Следовательно, область определения есть .

Исследуем поведение функции в окрестностях точек , :

, ,

Следовательно, точки , Являются точками разрыва второго рода.

Поскольку и , то здесь функция неограничена.

График функции пересекает координатные оси в только в начале координат, так как .

Функция не является периодичной.

Функция нечетная, так как область определения симметрична и , т. е.

Следовательно, график функции симметричен относительно начала координат и достаточно исследовать функцию для .

2) асимптоты графика функции. Поскольку односторонние пределы в точках , раны бесконечности, то прямые и являются вертикальными асимптотами графика функции.

Вычислим пределы:

Прямая является наклонной асимптотой графика функции.

3) точки возможного экстремума и интервалы монотонности функции. Находим первую производную функции:

Функция определена на . В промежутке производная обращается в нуль в точках , .

Определяем интервалы монотонности из неравенств и для любого .

Имеем:

, ,

Т. е. функция возрастает на .

Аналогично:

, ,

Т. е. функция убывает на .

4) промежутки выпуклости и вогнутости, точки перегиба. Вычисляем вторую производную функции :

Функция определена на области определения .

Находим интервалы вогнутости и выпуклости графика функции из неравенств , для любого .

Имеем:

Т. е. кривая вогнута на .

Аналогично:

Т. е. кривая выпукла на .

В точке имеем и в окрестности , а в окрестности . Значит, точка кривой с абсциссой отделяет интервал выпуклости кривой от ее интервала вогнутости. Поэтому является точкой перегиба кривой.

5) локальные экстремумы. Определяем с помощью второй производной локальные экстремумы. Так как , точка с абсциссой является точкой локального максимума. В силу симметрии графика функции точка с абсциссой является точкой локального минимума. Итак, , .

Результаты исследования функции заносим в таблицу 7.1.

Таблица 7.1 – Результаты исследования функции

0				3
0	+	Не сущ.	+	0	–
0	+	Не сущ.	–	–	–
0		Не сущ.		-4,5
(т. перег)

Исходя из результатов, содержащихся в таблице 7.1, строим график данной функции для . Используя нечетность функции, достраиваем ее график на всей области определения (рисунок 7.4).

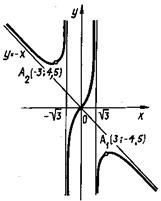
Рисунок 7.4 – График функции

< Предыдущая		Следующая >