05.3. Решение типовых примеров

1 Многочлен расположить по целым неотрицательным степеням .

Решение. Введем новую переменную . Тогда

.

Возвращаясь к переменной , получим

.

2 Представить функцию многочленом -й степени в окрестности точки и оценить погрешность.

Решение. 1 способ. Находим последовательно производную для данной функции:

,	,
,	,
,	,
,	,
,	,
,
,	,
.

Тогда формула Тейлора для функции в окрестности точки примет вид

,

Где , .

Преобразуя полученное выражение, имеем

.

Многочлен Тейлора функции имеет вид

.

Погрешность вычислений составит

,

Где , .

2 способ. Воспользуемся основным разложением в ряд Маклорена функции . Заменим в разложении на :

,

Где , .

3 Разложить по формуле Тейлора функцию в окрестности точки .

Решение. Воспользуемся основным разложением в ряд Маклорена функции . Заменим в разложении на

,

Где .

4 Разложить по формуле Маклорена функцию

.

Решение. Поскольку

.

В разложение 5 с остаточным членом в форме Пеано при имеем

.

При замене переменной на , получаем

,

А при замене на :

Тогда

==

.

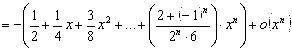5 Вычислить число с точностью .

Решение. Разложение функции в ряд Маклорена имеет вид:

, .

Заменив функцию многочленом Тейлора степени , получим приближенное равенство

,

Абсолютная погрешность которого

, .

Если рассматривать функцию для , то

.

Полагая , получаем приближенное значение числа

.

Чтобы определить, сколько нужно взять первых членов этой формулы для получения заданной точности, оценим величину остаточного члена

.

Имеем . Отсюда или .

Следовательно, при получим вычисленное значение числа с заданной точностью

< Предыдущая		Следующая >