04.4. Решение типовых примеров

1 Проверить, удовлетворяет ли условиям теоремы Ролля функция:

?

Решение. Преобразуем данную функцию к виду

.

Отсюда . Поэтому теорема Ролля применима на отрезках , и . Поскольку данная функция представляет собой многочлен, то она определена и непрерывна на каждом из отрезков. Найдем производную:

.

Очевидно, что для любых функция дифференцируема на соответствующих интервалах. Таким образом, теорема Ролля справедлива на отрезках , и .

2 Доказать, что уравнение не может иметь два различных действительных корня на интервале .

Решение. Предположим, что уравнение имеет два различных действительных корня и на данном интервале.

Рассмотрим функцию .

Тогда . При этом данная функция определена, непрерывна (как элементарная) на и дифференцируема на . Следовательно, по теореме Ролля существует точка такая, что .

С другой стороны, . Отсюда уравнение имеет единственный корень в точке , которая не принадлежит интервалу . Получили противоречие. Значит, уравнение не может иметь два различных действительных корня на .

3 Доказать, что , .

Решение. Рассмотрим функцию на отрезке .

Данная функция удовлетворяет условиям теоремы Лагранжа, поэтому по формуле Лагранжа

,

Где .

Поскольку , то .

4 Записав формулу Коши для функций и на отрезке , найти значение .

Решение. Данные функции определены и непрерывны на отрезке , а также дифференцируемы на интервале :

,

При этом .

Тогда по теореме Коши существует такая точка , что имеет место формула Коши

.

Подставляя, получим .

Решая данное уравнение относительно , находим

, .

5 Используя правило Лопиталя, вычислить пределы

А) ; г) ; ж) ;

Б) ; д) ; и) ;

В) ; е) ; к) .

Решение. а) имеем:

.

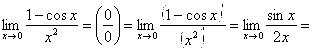
Б) имеем:

.

В) имеем:

.

Вычислим предел :

.

Тогда

.

Г) имеем:

.

Д) имеем:

.

Вычислим предел

.

Тогда

.

Е) имеем:

==

=

=.

Ж) имеем:

.

И) имеем:

.

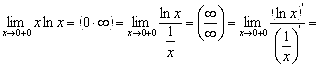
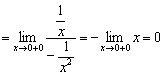К) имеем:

.

< Предыдущая		Следующая >