04.2. Теоремы Лагранжа и Коши

Теорема 2 (Лагранжа) Если функция непрерывна на отрезке и дифференцируема на интервале , то существует, по крайней мере, одна точка такая, что

.

Теорема Лагранжа называется также Теоремой о конечных приращениях, а приведенная формула – Формулой Лагранжа. Часто используется следующая запись формулы Лагранжа:

, .

Геометрический смысл теоремы Лагранжа. Выражение

Представляет собой угловой коэффициент хорды , а – угловой коэффициент касательной к кривой в точке . Теорема Лагранжа утверждает, что между точками и на дуге найдется, по крайней мере, одна точка , в которой касательная параллельна хорде , при условии, что в каждой точке дуги существует касательная (рисунок 4.2).

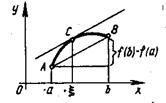
Рисунок 4.2 – Геометрический смысл

Теоремы Лагранжа

Физический смысл теоремы Лагранжа. Пусть – время, а – координаты точки, движущейся по прямой, в момент времени . В выражении

Величина в левой части равенства является средней скоростью движения точки по прямой за промежуток времени от до . Формула Лагранжа показывает, что существует такой момент времени , в котором мгновенная скорость равна средней скорости на временном отрезке .

Если в формуле Лагранжа положить , получим теорему Ролля, т. е. теорема Ролля является частным случаем теоремы Лагранжа.

Положим в формуле Лагранжа , . Тогда она примет вид

,

Где . Данная формула связывает приращения аргумента и функции, поэтому ее называют Формулой конечных приращений. Данная формула дает точное выражение приращения функции через вызвавшее его приращение аргумента в отличие от дифференциала функции, который определяет приближенное значение приращения функции: . В приближенных вычислениях приращение функции заменяют чаще дифференциалом, т. е. полагают . Формула Лагранжа применяется реже, так как для ее использования необходимо указать точку , что, вообще говоря, не всегда удается.

Обобщением теоремы Лагранжа является теорема Коши.

Теорема 3 (Коши) Пусть функции и удовлетворяют следующим условиям: непрерывны на отрезке ; дифференцируемы в интервале , причем . Тогда существует, по крайней мере, одна точка , такая, что

.

Если положить в формуле Коши , то все условия теоремы Коши будут выполнены, и формула Коши «перейдет» в формулу Лагранжа . Таким образом, теорема Лагранжа является частным случаем теоремы Коши.

< Предыдущая		Следующая >