03.4. Решение типовых примеров

1 Найти и , если функция задана параметрическими уравнениями:

Где .

Решение. Находим первую производную:

.

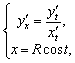
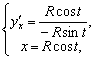
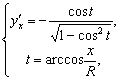
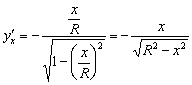Итак,

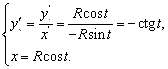
Тогда

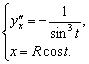
Отсюда

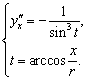
Следовательно,

.

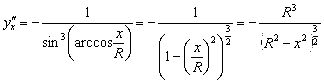2 Найти производную функции заданной неявно

Решение. Продифференцируем данное уравнение по переменной , считая, что есть функция от :

.

Отсюда

.

3 Найти производную -го порядка от функции .

Решение. Выполняя последовательное дифференцирование, получаем:

,

,

,

,

.

4 Найти производную второго порядка функции .

Решение. Находим первую производную данной функции:

Дифференцируя полученное выражение, получаем:

.

5 Найти производную второго порядка от функции , заданной уравнением: .

Решение. Найдем первую производную . Отсюда . Дифференцируя данное уравнение вторично, получим:

.

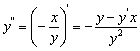Учитывая, что , имеем:

.

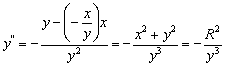< Предыдущая		Следующая >