01.3. Геометрический и физический смысл производной и дифференциала

Рассмотрим задачу о проведении касательной к произвольной плоской кривой. Пусть – дуга плоской кривой, – точка этой кривой, – секущая (рисунок 1.1). Если точка движется по кривой к точке , то секущая поворачивается вокруг точки и стремится к некоторому предельному положению .

Касательной к кривой в точке называется прямая , которая представляет собой предельное положение секущей при стремлении по кривой точки к точке (рисунок 1.1).

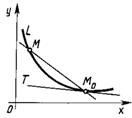
Рисунок 1.1 – Секущая

И касательная

Если предельного положения секущей не существует, то говорят, что в точке провести касательную нельзя. Это бывает в случае, когда точка является Точкой излома, или Заострения, кривой (рисунок 1.2, а, б, в).

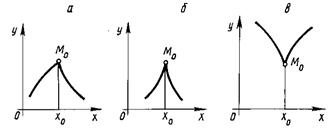
Рисунок 1.2 – Точки излома графика функции

Пусть кривая является графиком функции и точка (рисунок 1.3).

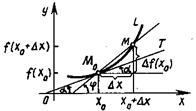
Рисунок 1.3 – Геометрический смысл касательной

Предположим, что касательная к кривой в точке существует. Угловой коэффициент секущей есть

.

Если , то точка движется по кривой к точке и секущая стремится к своему предельному положению . Таким образом,

. (1.2)

Отсюда следует Геометрический Смысл производной: производная от функции при равна угловому коэффициенту касательной к графику функции в точке с абсциссой .

Уравнение касательной имеет вид

. (1.3)

Так как угловые коэффициенты касательной и нормали связаны условием перпендикулярности , то Уравнение нормали в точке имеет вид:

. (1.4)

Углом между кривыми называют угол между касательными к кривым в точке их пересечения.

Геометрический смысл дифференциала: дифференциал функции в точке изображается приращением ординаты точки касательной, проведенной в к линии (рисунок 1.4).

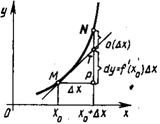
Рисунок 1.4 – Геометрический смысл дифференциала

Рассмотрим функцию , определенную и непрерывную в некоторой окрестности точки . Если аргумент функции получает приращение (положительное или отрицательное), такое, что принадлежит той же окрестности точки , то соответствующее приращение функции равно . Тогда средняя скорость изменения функции равна:

, (1.5)

А мгновенная скорость ее изменения:

. (1.6)

Механический смысл производной: производная – математическая модель мгновенной скорости процесса, описываемого функцией .

В зависимости от содержательной сущности функции можно получить широкий круг математических моделей скорости протекания процессов. Рассмотрим некоторые из них.

1 Пусть материальная точка движется неравномерно и – функция, устанавливающая зависимость пути от времени . Тогда мгновенная скорость движения в момент времени есть производная от пути по времени :

.

Дифференциал равен пути, который прошла бы рассматриваемая точка за промежуток времени , начиная с момента , если движение на этом участке равномерно со скоростью . Этот путь отличается от истинного пути на бесконечно малую более высокого порядка, чем : при .

2 Пусть – функция, описывающая процесс изменения скорости неравномерного движения в зависимости от времени . Тогда мгновенное ускорение материальной точки в фиксированный момент времени есть производная от скорости по времени :

.

3 Пусть – функция, описывающая процесс изменения количества теплоты, сообщаемой телу при нагревании его до температуры . Тогда теплоемкость тела есть производная от количества теплоты по температуре :

.

4 Пусть необходимо определить линейную плотность неоднородного тонкого стержня длиной , где – масса стержня, концы которого имеют координаты и (предполагается, что ось направлена по стержню). Ясно, что масса стержня является функцией : . Тогда линейная плотность неоднородного тонкого стержня в точке есть производная от массы по длине :

.

5 Пусть – функция, описывающая процесс изменения магнитного потока в зависимости от времени . Тогда мгновенное значение электродвижущей силы индукции равно скорости изменения магнитного потока, т. е. производной от магнитного потока по времени :

6 Пусть – функция, описывающая процесс изменения заряда в колебательном контуре в зависимости от времени . Тогда сила тока в контуре в момент времени равна производной заряда по времени :

.

Дифференциал равен количеству электричества, которое бы протекало через поперечное сечение проводника за промежуток времени , если бы сила тока была постоянной и равной силе тока в момент времени . При этом при .

< Предыдущая		Следующая >