2. Бесконечно малые и бесконечно большие последовательностии их свойства

Определение 1. Бесконечно малой последовательностью называется такая последовательность, предел которой равен нулю, т. е. – бесконечно малая последовательность, если

.

Если не пользоваться понятием предела последовательности, то определение бесконечно малой последовательности можно сформулировать так: последовательность называется бесконечно малой, если для всякого можно подобрать такой номер , начиная с которого все члены последовательности удовлетворяют неравенству

. (3)

Последовательность, все члены которой равны нулю, также называется бесконечно малой.

Пример 5. Показать, что последовательность 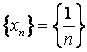– бесконечно малая.

Решение. Показать, что предел при равен 0. Пусть задано любое . Рассмотрим неравенство

, или ,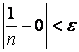

Откуда , т. е. как только номер членов последовательности , где , имеет место неравенство 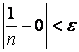. Следовательно,

,

Т. е. последовательность 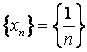– бесконечно малая.

< Предыдущая		Следующая >