2.1. Основные свойства бесконечно малых последовательностей

1. Бесконечно малая последовательность есть ограниченная последовательность.

2. Алгебраическая сумма конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

3. Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность .

4. Частное от деления бесконечно малой последовательности на число есть бесконечно малая последовательность .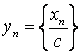

Определение 2. Последовательность называется бесконечно большой, если для всякого как угодно большого числа можно указать такой номер , начиная с которого все последующие члены последовательности удовлетворяют неравенству

. (4)

Если последовательность бесконечно большая, то пишут

при или

(читают: « стремится к бесконечности при , стремящемся к бесконечности, или предел при , стремящемся к бесконечности, равен бесконечности»).

Бесконечно большая последовательность может принимать, начиная с некоторого номера, только положительные значения (тогда пишут при или ) либо только отрицательные (тогда пишут при или ).

Символ ( или ) не является числом, а употребляется лишь для условной краткой записи предложения: «величина в процессе изменения по абсолютному значению неограниченно возрастает». Поэтому не является равенством (а только символической записью), так как не является числом. Говорить о каких-либо действиях на не имеет смысла, однако пользоваться символическими записями с помощью удобно.

< Предыдущая		Следующая >