2.2. Основные свойства бесконечно больших последовательностей
1. Арифметическая сумма нескольких бесконечно больших последовательностей одного знака есть бесконечно большая последовательность: например, если ![]() при
при ![]() и
и ![]() при
при ![]() , то и
, то и ![]() при
при ![]() ; если
; если ![]() при
при ![]() и
и ![]() при
при ![]() , то и
, то и ![]() при
при ![]() .
.
2. Сумма бесконечно большой последовательности и ограниченной последовательности есть последовательность бесконечно большая.
Если ![]() при
при ![]() , а
, а ![]() , где
, где ![]() – постоянная величина, то
– постоянная величина, то ![]() при
при ![]() .
.
3. Произведение бесконечно большой последовательности ![]() на постоянное число
на постоянное число ![]() есть бесконечно большая последовательность.
есть бесконечно большая последовательность.
Если ![]() при
при ![]() и
и ![]() - постоянная величина, то
- постоянная величина, то ![]() при
при ![]() .
.
4. Частное от деления бесконечно большой последовательности ![]() на постоянное число
на постоянное число ![]() есть бесконечно большая последовательность.
есть бесконечно большая последовательность.
Если ![]() при
при ![]() и
и ![]() - постоянная величина, то
- постоянная величина, то ![]() при
при ![]() .
.
5. Если последовательность ![]() – бесконечно большая, причем
– бесконечно большая, причем ![]() ни при каком
ни при каком ![]() , то последовательность
, то последовательность ![]() – бесконечно малая. Наоборот, если последовательность
– бесконечно малая. Наоборот, если последовательность ![]() – бесконечно малая, причём
– бесконечно малая, причём ![]() ни при каком
ни при каком ![]() , то последовательность
, то последовательность ![]() – бесконечно большая.
– бесконечно большая.
Если ![]() при
при ![]() , причём
, причём ![]() при всех значениях
при всех значениях ![]() , то
, то 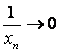 при
при ![]() . Если
. Если ![]() при
при ![]() , причём
, причём ![]() при всех значениях
при всех значениях ![]() , то
, то 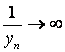 при
при ![]() .
.
6. Частное ![]() от деления ограниченной последовательности
от деления ограниченной последовательности ![]() на бесконечно большую последовательность
на бесконечно большую последовательность ![]() есть бесконечно малая последовательность. Если
есть бесконечно малая последовательность. Если ![]() , где
, где ![]() – некоторое положительное число, и
– некоторое положительное число, и ![]() при
при ![]() , то
, то ![]() – бесконечно малая последовательность, т. е.
– бесконечно малая последовательность, т. е. 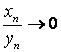 при
при ![]() . В частности, частное от деления бесконечно малой последовательности на бесконечно большую последовательность есть бесконечно малая последовательность.
. В частности, частное от деления бесконечно малой последовательности на бесконечно большую последовательность есть бесконечно малая последовательность.
Пример 6. Доказать, что последовательность ![]() есть бесконечно большая при
есть бесконечно большая при ![]() .
.
Решение. Возьмем произвольное число ![]() и решим неравенство
и решим неравенство ![]() . Прологарифмировав, получим
. Прологарифмировав, получим ![]() . Если взять
. Если взять ![]() , то для всех
, то для всех ![]() будет выполняться неравенство
будет выполняться неравенство ![]() , а это значит, что последовательность бесконечно большая.
, а это значит, что последовательность бесконечно большая.
| < Предыдущая | Следующая > |
|---|