3.4. Метод Ньютона в многомерном случае

Пусть задана система нелинейных уравнений

Или в более компактной форме: F(X)=0, где ─-мерная вектор-функция (вектор-столбец).

Для реализации метода решения и исследования сходимости необходимо, чтобы функции были достаточно гладкими, например, , где .

Рассмотрим I-ое уравнение системы: И пусть - некоторое приближение к корню , полученное на K-ой итерации.

Разложим функцию в многомерный ряд Тейлора в точке :

,

(17)

Где

-

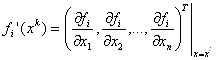- вектор-градиент функции в точке , а - скалярное произведение векторов A и B. Пренебрегая остаточным членом в (17), положим

Или в более компактной матричной форме:

,

(18)

Где

-

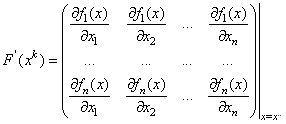- так называемая матрица Якоби первых производных в точке .

Пусть . Разрешим систему линейных алгебраических уравнений (18) относительно X:

И положим :

(19)

Векторное уравнение (19) представляет собой Итерационную процедуру Ньютона в многомерном случае. Для ее запуска необходимо задать начальную точку . Однако при произвольном выборе начальной точки нельзя гарантировать сходимость процедуры Ньютона. Вопрос о сходимости (19) в теоретическом плане более сложный, чем тот же вопрос о сходимости метода Ньютона в одномерном случае. Рассмотрим некоторые основные моменты проблемы исследования сходимости процедуры (19).

Прежде всего отметим, что для реализации метода Ньютона необходимо, чтобы матрица Якоби была невырождена в некоторой окрестности точки . Тогда обратная матрица существует в этой окрестности. Аналогично одномерному случаю, процедуру (19) можно рассматривать как итерационный поиск неподвижной точки для уравнения

,

Где - -Мерная оператор-функция. Можно показать, что . Поэтому, как и в одномерном случае существует окрестность точки , в которой оператор-функция является сжимающим оператором с некоторой константой сжатия , тем меньшей, чем ближе точка к точке (в эвклидовой норме). Поэтому о характере сходимости многомерного метода Ньютона справедливы утверждения, аналогичные одномерному случаю.

Например, если - строго выпукла в G, и начальное приближение выбирается достаточно близко к , то итерационная процедура Ньютона (19) сходится с линейной скоростью, а, начиная с некоторого номера, - и с квадратичной скоростью.

Замечание. Строгую формулировку достаточных условий сходимости метода Ньютона в многомерном случае можно найти в цитируемой литературе (см., например, [2]). На практике эти условия, как правило, проверить чрезвычайно сложно. Поэтому при работе на компьютере (например, в пакете MATLAB) используют Метод проб и ошибок при выборе начальной точки . На начальном этапе важно найти так называемую Зону притяжения, т. е. такую область , что при выборе процедура (19) сходится.

Пример 4. Задана система уравнений:

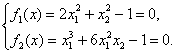
Взяв в качестве начального приближения точку , выполнить одну итерацию по методу Ньютона.

Ответ: . Точное решение: .

< Предыдущая		Следующая >