3.3. Метод Ньютона

Пусть снова задано уравнение F(X)=0. Запишем его в виде ,

Где положим .

Пусть Хк – некоторое приближение к корню Х*. Для ускорения сходимости итераций желательно, чтобы был как можно меньше. Положим

Отсюда находим, что . Подставляя в исходное уравнение, получаем рекуррентную формулу:

, . (11)

Это и есть Итерационная процедура Ньютона.

Метод Ньютона известен и под другим названием: Метод касательных. Дадим графическую иллюстрацию данного метода.

Пусть и строго выпукла (т. е. ). Пусть, кроме того, - единственный корень функции на промежутке .

В качестве начального приближения возьмем точку , такую, для которой . Проведем через точку на плоскости касательную к кривой . Запишем уравнение касательной: . В качестве следующего приближения возьмем точку , в которой . Отсюда находим

. Далее в точке графика проводим новую касательную, и т. д. В результате получаем итерационную процедуру Ньютона (11).

Метод касательных проиллюстрирован на рис.3.2.

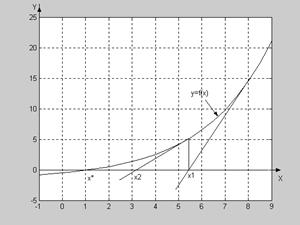Рис.3.2. Графическая иллюстрация метода Ньютона (метода касательных). Начальная точка X0 = 8. Точное значение корня X* = 1. X1 и X2 – два последовательных приближения к корню, полученные с помощью касательных.

Исследуем условия сходимости метода Ньютона.

Теорема 3.5. Пусть , на , и имеет единственный действительный корень на . Тогда , такое, что на множестве

Процедура Ньютона (1) сходится к точке со скоростью геометрической прогрессии, а в некоторой малой окрестности точки X* и с квадратичной скоростью.

В силу непрерывности функций на [A,B], обе производные ограниченыпоэтому , причем по условию.

Заметим, что итерационная процедура (11) равносильна методу простых итераций для уравнения

(12)

Очевидно, что является неподвижной точкой функционального оператора , называемого Операторной функцией Ньютона-Рафсона. Проверим условия сжатости данной функции. Для этого вычислим и оценим производную . Имеем:

Оценивая полученное равенство по модулю, и учитывая условия теоремы, получим

(13)

Поскольку - корень уравнения , то, как следует из неравенства (13),

и близка к нулю в некоторой малой окрестности точки , где и следует ожидать выполнения условия сжатости.

Запишем формулу конечных приращений Лагранжа

Оценивая по модулю, получаем

Подставляя эту оценку в (13), получаем:

Условие сжатости будет, очевидно, выполнено, если

. (14)

Обозначив , получаем конкретизацию окрестности , где выполняется одно из условий сжатости. Пусть теперь найдено -е приближение к корню .

Так как по условию теоремы непрерывна на , то справедливо тэйлоровское разложение функции с центром в точке с остаточным членом в форме Лагранжа

Положим в последнем равенстве :

Выражая отсюда , получим:

(15)

Вычтем (15) из (11):

;

Оценивая последнее равенство по модулю, получаем:

(16)

Продолжим далее оценку по модулю, используя (14):

Таким образом, если , где определяется из неравенства (14), то точка . Следовательно, выполняется и второе условие теоремы 3.4, а значит последовательность сходится к корню со скоростью геометрической последовательности (т. е. линейно). Далее из неравенства (16) следует, что как только при некотором выполнится условие , так в дальнейшем, при сходимость становится квадратичной: