6.3. Метод Рунге-Кутта
Изложим идею метода на примере задачи Коши:
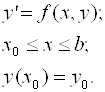 (6.7)
(6.7)
Интегрируя это уравнение в пределах от X до X + H (0 < H <1), получим равенство
 (6.8)
(6.8)
Которое посредством последнего интеграла связывает значения решения рассматриваемого уравнения в двух точках, удаленных друг от друга на расстояние шага H.
Для удобства записи выражения (6.8) используем обозначение
∆Y = Y(X + H) – Y(X) и замену переменной интегрирования T = X + AH. Окончательно получим:
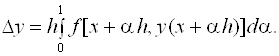 (6.9)
(6.9)
Указав эффективный метод приближенного вычисления интеграла в выражении (6.9), мы получим при этом одно из правил численного интегрирования уравнения (6.7).
Постараемся составить линейную комбинацию величин jI,
I = 0, 1, ..., Q, которая будет являться аналогом квадратурной суммы и позволит вычислить приближенное значение приращения DY:
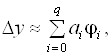 (6.10)
(6.10)
Где
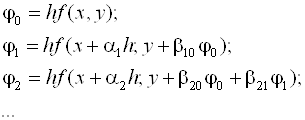
Метод четвертого порядка для Q = 3, являющийся аналогом широко известной в литературе четырехточечной квадратурной формулы "трех восьмых", имеет вид
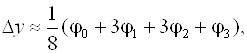 (6.11)
(6.11)
Где

Особо широко известно другое вычислительное правило типа Рунге-Кутта четвертого порядка точности:
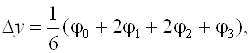 (6.12)
(6.12)
Где
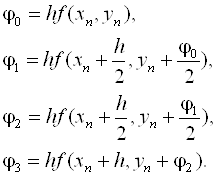
Метод Рунге-Кутта имеет погрешность четвертого порядка (~ H4 ).
Правило Рунге. Если приближенный метод имеет порядок погрешности M, то погрешность можно приближенно оценить по формуле
 (6.13)
(6.13)
В формуле (6.13) O(Xi) – главный член погрешности, ![]() И
И ![]() - приближенные решения в точке Xi, найденные с шагом H и 2H соответственно.
- приближенные решения в точке Xi, найденные с шагом H и 2H соответственно.
Пример 6.1. Решить дифференциальное уравнение 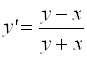 на отрезке [0, 1] c начальным условием Y(X=0) = 1. Найти первые три точки, приняв шаг H = 0.05.
на отрезке [0, 1] c начальным условием Y(X=0) = 1. Найти первые три точки, приняв шаг H = 0.05.
Решение. Поставленная задача была решена методом разложения в ряд Тейлора (6.3); методом Эйлера (6.6) и методом Рунге-Кутта (6.12). Для наглядности все полученные результаты сведем в табл. 6.1.
Таблица 6.1
|
Xi |
Ряд Тейлора (m=1) |
Метод Эйлера |
Метод Рунге-Кутта | |||||
|
Yi |
Yi |
Yi |
F(xi, yi) |
φ0 |
φ1 |
φ2 |
φ3 | |
|
0 |
1 |
1 |
1 |
1 |
- |
- |
- |
- |
|
0.05 |
1.05 |
1.05 |
1.0477 |
0.9089 |
0.05 |
0.0477 |
0.0476 |
0.0454 |
|
0.1 |
1.1 |
1.0931 |
1.0912 |
0.8321 |
0.0454 |
0.0435 |
0.0434 |
0.0416 |
|
0.15 |
1.15 |
1.1347 |
1.1311 |
0.7658 |
0.0416 |
0.0399 |
0.0399 |
0.0383 |
| < Предыдущая | Следующая > |
|---|