6.4. Многошаговые методы

Ранее нами были рассмотрены одношаговые методы решения задачи Коши. Эти методы, обладая рядом удобных для практики вычислений особенностей, страдают одним существенным недостатком. При построении этих методов привлекается информация о решаемой задаче только на отрезке длиной в один шаг, поэтому подобная информация на каждом этапе процесса должна быть получена заново, что предопределяет большую трудоемкость соответствующих вычислительных правил.

Если отказаться от требования одношаговости, можно вычислительные методы строить таким образом, чтобы часть получаемой информации могла быть использована повторно на нескольких следующих шагах вычислительного процесса. Такие методы, использующие информацию о решаемой задаче на отрезке длиной более одного шага, и называются многошаговыми.

Будем, как и раньше рассматривать задачу Коши:

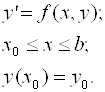(6.14)

Ограничимся рассмотрением многошаговых методов с равномерной сеткой:

Xi = x0 + ih; i = 0, 1,..., n; n·h = b - x0. (6.15)

Рассмотрим вычислительные правила вида

(6.16)

Среди вычислительных правил вида (6.16) особенно широко известны Экстраполяционные (при S = 0) и Интерполяционные (при S = 1, A-1 ¹ 0).

< Предыдущая		Следующая >