6.2. Метод рядов, не требующий вычисления производных. правой части уравнения

Естественно поставить задачу о таком усовершенствовании приведенного выше одношагового метода, которое сохраняло бы основные его достоинства, но не было бы связано с нахождением значений производных правой части уравнения

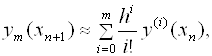(6.5)

Где Xn+1 = Xn + H.

Чтобы выполнить это условие (последнее), производные Y(I)(X),
I = 2, 3,..., M, входящие в правую часть уравнения (6.5), можно заменить по формулам численного дифференцирования их приближенными выражениями через значение функции Y' и учесть, что Y'(X) = F [X, Y(X)].

В случае M = 1 приближенное равенство (6.5) не требует вычисления производных правой части уравнения и позволяет с погрешностью порядка H2 находить значение Y(Xn+ H) решения этого уравнения по известному его значению Y(Xn). Соответствующее одношаговое правило можно записать в виде

(6.6)

Это правило (6.6) впервые было построено Эйлером и носит его имя. Иногда его называют также правилом Ломаных или методом Касательных. Метод Эйлера имеет простую геометрическую интерпретацию (см. рис. 6.2).

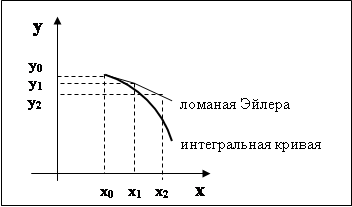
Рис. 6.2. Нахождение решения методом Эйлера

Замечание Метод Эйлера имеет порядок точности ~ H2 На одном шаге. Практическая оценка погрешности приближенного решения может быть получена по Правилу Рунге.

< Предыдущая		Следующая >