6.1. Решение обыкновенных дифференциальных уравнений. Методы решения задачи Коши

Среди задач, с которыми приходится иметь дело в вычислительной практике, значительную часть составляют различные задачи, сводящиеся к решению обыкновенных дифференциальных уравнений. Обычно приходится прибегать к помощи приближенных методов решения подобных задач. В случае обыкновенных дифференциальных уравнений в зависимости от того, ставятся ли дополнительные условия в одной или нескольких точках отрезка изменения независимой переменной, задачи обычно подразделяются на Одноточечные (задачи с начальными условиями или Задачи Коши) и Многоточечные. Среди многоточечных задач наиболее часто в прикладных вопросах встречаются так называемые Граничные задачи, когда дополнительные условия ставятся на концах рассматриваемого отрезка.

В дальнейшем ограничимся рассмотрением численных методов решения задачи Коши. Для простоты изложения методов решения задачи будем рассматривать случай одного обыкновенного дифференциального уравнения первого порядка.

Пусть на отрезке X0 £ X £ B требуется найти решение Y(X) дифференциального уравнения

, (6.1)

Удовлетворяющее при X = X0 начальному условию

(6.2)

Будем считать, что условия существования и единственности решения поставленной задачи Коши выполнены.

На практике найти общее либо частное решение задачи Коши удается крайне редко, поэтому приходится решать эту задачу приближенно. Отрезок [X0, B] накрывается сеткой (разбивается на интервалы) чаще всего с постоянным шагом H ( H = Xn+1 - Xn ), И по какому-то решающему правилу находится значение Yn+1 = Y(Xn+1). Таким образом, в качестве решения задачи Коши численными методами мы получаем таблицу, состоящую из двух векторов:
X = (X0 , X1 , …Xn) – Вектора аргументов и соответствующего ему вектора функции Y = ( Y0 , Y1,… Yn ).

Численные методы (правила), в которых для нахождения значения функции в новой точке используется информация только об одной (предыдущей) точке, называются Одношаговыми.

Численные методы (правила), в которых для нахождения значения функции в новой точке используется информация о нескольких (предыдущих) точках, называются Многошаговыми.

Из общего курса обыкновенных дифференциальных уравнений широкое распространение получил аналитический метод, основанный на идее разложения в ряд решения рассматриваемой задачи Коши. Особенно часто для этих целей используется ряд Тейлора. В этом случае вычислительные правила строятся особенно просто. При этом приближенное решение Ym(X) исходной задачи ищут в виде

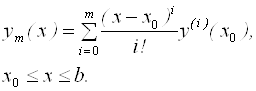(6.3)

Здесь а значения I = 2, 3,…M находят по формулам, полученным последовательным дифференцированием уравнения (6.1):

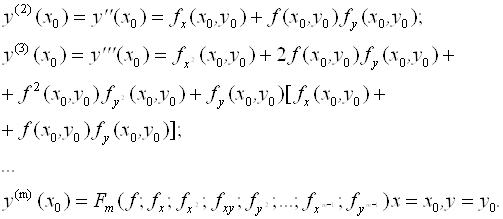(6.4)

Для значений X, близких к X0, метод рядов (6.3) при достаточно большом значении M дает обычно хорошее приближение к точному решению Y(X) задачи (6.1). Однако с ростом расстояния êX - X0 ê погрешность приближенного равенства Y(X) » Ym(X), вообще говоря, возрастает по абсолютной величине, и правило (6.3) становится вовсе неприемлемым, когда X выходит из области сходимости соответствующего ряда (6.3) Тейлора.

Если в выражении (6.3) ограничиться M = 1, То для вычисления новых значений Y(X) нет необходимости пересчитывать значение производной, правда и точность решения будет невысока. Графическая интерпретация этого метода приведена на рис. 6.1.

 

 

 

 

 

 

 

 

 

Рис. 6.1. Разложение функции в ряд Тейлора (m=1)

< Предыдущая		Следующая >