5.2. Метод градиента (метод скорейшего спуска)
Пусть имеется система нелинейных уравнений:
 (5.13)
(5.13)
Систему (5.13) удобнее записать в матричном виде:
![]() (5.14)
(5.14)
Где  - вектор – функция;
- вектор – функция; 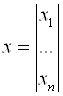 - вектор – аргумент.
- вектор – аргумент.
Решение системы (5.14), как и для системы линейных уравнений (см. п. 3.8), будем искать в виде
![]() (5.15)
(5.15)
Здесь ![]() и
и ![]() - векторы неизвестных на P и P+1 шагах итераций; вектор невязок на P-ом шаге – F(P) = F(X(P)); W'P – транспонированная матрица Якоби на P – ом шаге;
- векторы неизвестных на P и P+1 шагах итераций; вектор невязок на P-ом шаге – F(P) = F(X(P)); W'P – транспонированная матрица Якоби на P – ом шаге;
 ;
;
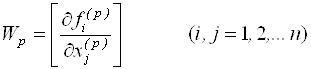 .
.
Пример 5.2. Методом градиента вычислим приближенно корни системы
![]()
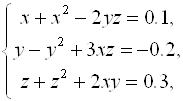
Расположенные в окрестности начала координат.
Имеем:

Выберем начальное приближение:

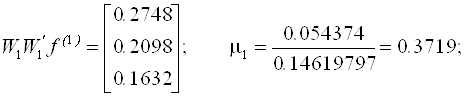
По вышеприведенным формулам найдем первое приближение:
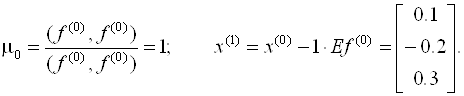
Аналогичным образом находим следующее приближение:
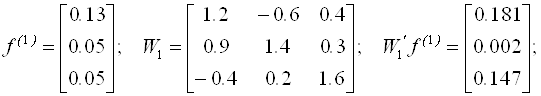
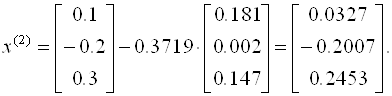
Ограничимся двумя итерациями (шагами), и оценим невязку:

Замечания
· Как видно из примера, решение достаточно быстро сходится, невязка быстро убывает.
· При решении системы нелинейных уравнений методом градиента матрицу Якоби необходимо пересчитывать на каждом шаге (итерации).
Вопросы для самопроверки
· Как найти начальное приближение: а) для метода Ньютона; б) для метода градиента?
· В методе скорейшего спуска вычисляется Якобиан (матрица Якоби). Чем отличается Якобиан, вычисленный для СЛАУ, от Якобиана, вычисленного для нелинейной системы уравнений?
· Каков критерий остановки итерационного процесса при решении системы нелинейных уравнений: а) методом Ньютона; б) методом скорейшего спуска?
| < Предыдущая | Следующая > |
|---|