4.5. Метод Ньютона (метод касательных)
Пусть корень ξ Уравнения
F(X) = 0, (4.13)
Отделен на отрезке [A, B], причем первая и вторая производные F¢(X) и F¢¢(X) непрерывны и сохраняют определенные знаки при ![]() . Найдя какое-нибудь N-ое приближение корня
. Найдя какое-нибудь N-ое приближение корня ![]() , мы можем уточнить его по методу Ньютона следующим образом. Пусть
, мы можем уточнить его по методу Ньютона следующим образом. Пусть
ξ = Xn + Hn, (4.14)
Где Hn - величина малая. Отсюда по формуле Тейлора получим (ограничиваясь первым порядком малости относительно Hn)
F(Xn + Hn) = F(Xn) + Hn F¢(Xn) = 0. (4.15)
Следовательно,
Hn = - F(Xn) / F¢ (Xn). (4.16)
Подставив полученное выражение в формулу (4.14), найдем следующее (по порядку) значение корня:
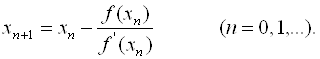 (4.17)
(4.17)
Проиллюстрируем графически нахождение корня методом Ньютона (рис. 4.3.).
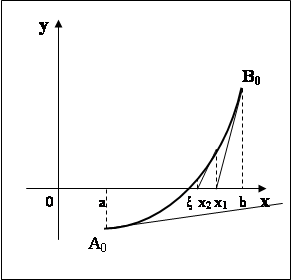 |
Рис. 4.3. Уточнение корня методом касательных
Если в качестве начального приближения выбрать точку Х0 = В0 , то процесс быстро сходится. Если же выбрать точку Х0 = А0, то Х1 ![]() [A, b], И процесс нахождения корня расходится. Рекомендуется: в качестве Х0 выбрать точку, где F(x)·f¢¢(x) > 0.
[A, b], И процесс нахождения корня расходится. Рекомендуется: в качестве Х0 выбрать точку, где F(x)·f¢¢(x) > 0.
| < Предыдущая | Следующая > |
|---|