4.6. Комбинированный метод

Пусть F(A)·F(B) < 0, а F¢(X) и F¢¢(X) сохраняют постоянные знаки на отрезке [A¸ b]. Соединяя метод хорд и метод касательных, получаем метод, на каждом шаге которого находим значения по недостатку и значения по избытку точного корня ξ уравнения F(X) = 0. Теоретически здесь возможны четыре случая:

· F¢(x) > 0; F¢¢(X) > 0;

· F¢(x) > 0; F¢¢(X) < 0;

· F¢(x) < 0; F¢¢(X) > 0;

· F¢(x) < 0; F¢¢(X) < 0.

Рассмотрим только первый случай, так как остальные три ведут себя аналогично и могут быть сведены к первому.

Итак, пусть F¢(X) > 0 и F¢¢(X) > 0 при . Полагаем, что (для метода хорд), (для метода касательных). Тогда новые значения корня вычисляем по формулам

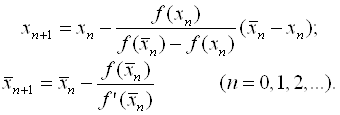(4.18)

Рис. 4.4 наглядно иллюстрирует суть комбинированного метода.

 

Рис. 4.4. Уточнение корня комбинированным методом

Доказано, что . Следует обратить внимание на то, что на каждом шаге метод хорд применяется к новому отрезку . Если задать максимальное значение погрешности ε > 0, Процесс уточнения значения корня продолжаем до тех пор, пока не выполнится условие

. (4.19)

Пример 4.1. Вычислить с точностью до 0.0005 положительный корень уравнения

F(X) = X5 – X – 0.2 = 0.

На первом этапе отделения корней выбрали интервал [1.0, 1.1], на концах которого функция имеет противоположные знаки. Действительно,
F(1) = – 0.2 < 0, F(1.1) = 0.31051 > 0. В выбранном нами интервале F¢¢(X) > 0, F¢¢(X) > 0, то есть знаки производных сохраняются.

Применим комбинированный метод, приняв . По формулам (4.18) вычислим

.

Так как точность недостаточная (погрешность велика), вычислим следующие значения:

Таким образом, за два шага мы обеспечили требуемую точность.

Замечания

· Комбинированный метод наиболее трудоемок.

· Метод, как и метод Ньютона не всегда сходится (почему?).

· Комбинированный метод сходится быстрее всех ранее рассмотренных, (если он сходится).

Вопросы для самопроверки

· Какие точные методы решения нелинейных уравнений вы знаете?

· Для чего нужен первый этап - отделение корней?

· Сформулируйте условия существования решения уравнения. Являются ли эти требования необходимыми и достаточными?

· Что можно сказать о точности методов половинного деления, хорд, касательных и комбинированного? По каким параметрам их еще можно сравнить?

· В соответствии с известной теоремой на отрезке [A, B] Существует решение. Всегда ли его можно найти методом половинного деления, методом хорд, и т. п.?

< Предыдущая		Следующая >