3.6. Метод простой итерации (метод Якоби)

Рассмотрим систему

A·X = F, (3.27)

Где матрица A = [Aij] (I,J = 1, 2, …M) имеет обратную матрицу;
X = (X1, X2, X3,…Xm) – вектор неизвестных, F – вектор свободных членов.

Преобразуем систему (3.27) к следующему виду:

(I = 1, 2, …M), (3.28)

Где , , при этом предполагаем, что .

Условимся, как обычно, считать значение суммы равным нулю, если верхний предел суммирования меньше нижнего. Тогда при I = 1 уравнение (3.28) имеет вид

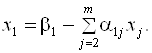(3.29)

В методе простой итерации (методе Якоби) исходят из записи системы в виде (3.28), итерации при этом определяют следующим образом:

(3.30)

Начальные значения – (I = 0, 1, … M) задаются произвольно. Окончание итерационного процесса определяют либо заданием максимального числа итераций N0, либо следующим условием:

(3.31)

Где ε > 0.

В качестве нулевого приближения в системе (3.30) примем

. (3.32)

Если последовательность приближений X1(0), X2(0), ..., Xm(0), X1(1), X2(1), ..., Xm(1), ..., X1(K), X2(K), ..., Xm(K) имеет предел

, (3.33)

То этот предел является решением системы (3.28).

Достаточным условием сходимости решения системы (3.27) является то, что матрица A является матрицей с преобладающими диагональными элементами, то есть

(3.34)

< Предыдущая		Следующая >