3.5. Вычисление определителей методом Гаусса

. (3.23)

Необходимо вычислить D = det A.

Вспомним свойства определителей:

· для того чтобы умножить (разделить) определитель на какое либо число, достаточно умножить (разделить) на это число строку или столбец:

; (3.24)

· значение определителя не изменится, если его строку заменить суммой этой строки и другой, умноженной на произвольное число.

Учитывая это свойство, умножая первую строку последовательно на A21, a31, ..., an1 и вычитая из второй, третьей и т. д., получим

; (3.25)

· величина определителя равна сумме произведений элементов строки (столбца) на (-1)i+j |A|i j, где |A|i j – соответствующие миноры.

Используя это свойство, представим определитель как сумму произведений элементов первого столбца на соответствующие миноры. При этом учтем, что за исключением первого элемента значения остальных элементов столбца равны нулю.

Таким образом, мы понизили порядок определителя на 1. Применим к полученному определителю порядка N - 1 такие же преобразования. Выполняя N шагов, найдем определитель D как произведение ведущих элементов:

(3.26)

Пример 3.5.

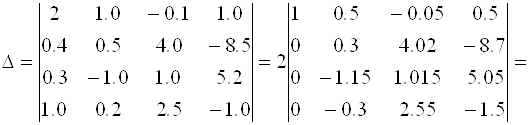
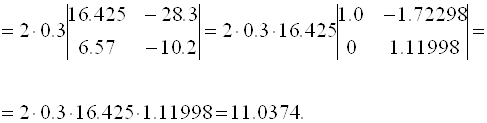
Замечания

· При наличии решения, точные методы всегда дадут его через конечное число шагов.

· В рамках точных методов вычислительная погрешность увеличивается с ростом размеров СЛАУ и не может быть уменьшена.

< Предыдущая		Следующая >