3.4. Вычисление обратной матрицы методом Гаусса
Пусть дана неособенная матрица
A = [Aij] (I, j = 1,2, ..., N). (3.19)
Необходимо найти её обратную матрицу
A-1 = [Xij] (I,J = 1,2, ..., N). (3.20)
Вспомним основное соотношение линейной алгебры:
A·A-1 = E, (3.21)
Где Е – единичная матрица.
Перемножая матрицы A и A-1, получаем N2 уравнений относительно N2 неизвестных XiJ:
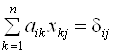 (I,J = 1, 2, ..., N), (3.22)
(I,J = 1, 2, ..., N), (3.22)
Где 
Таким образом, получим N систем линейных уравнений для J = 1, 2, ..., N, имеющих одну и ту же матрицу коэффициентов A и различные столбцы - свободные члены, которые можно Одновременно решить методом Гаусса.
Рассмотрим это подробнее, вычислив матрицу, обратную ![]() :
:
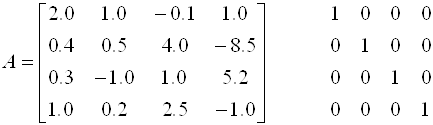
Разделив все коэффициенты первой строки на A11 = 2, Получим первую главную строку (Обратите внимание, что с N Столбцами свободных членов проводятся те же действия, что и с одним):
1.0 0.5 -0.05 0.5 0.5 0 0 0
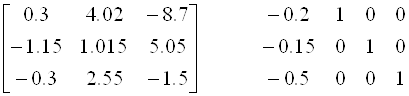
1.0 13.4 -29 -0.6667 3.333 0 0
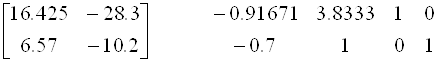
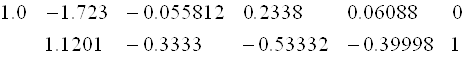
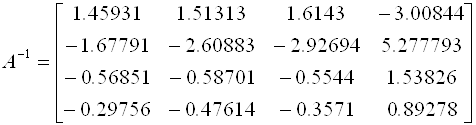 .
.
Для проверки перемножим полученную обратную матрицу и исходную (должны получить единичную):
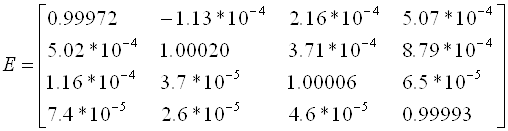 .
.
Благодаря округлению, убеждаемся, что обратная матрица вычислена неточно. В дальнейшем можно показать, как методом простой итерации можно уточнить A-1.
| < Предыдущая | Следующая > |
|---|