3.3. Схема Гаусса с выбором главного элемента

Рассмотрим СЛАУ

(3.17)

Запишем расширенную прямоугольную матрицу коэффициентов системы (3.17):

. (3.18)

Среди элементов матрицы Aij (I,J = 1, ...N) выберем наибольший по модулю, называемый Главным элементом. Пусть им будет, например, элемент Apq. Строка, содержащая главный элемент, называется Главной строкой.

Далее вычисляем множители Mi = Aiq / Apq для всех I ¹ P.Затем преобразуем матрицу (3.18) следующим образом: из каждой I-ой неглавной строки вычитаем почленно главную строку, умноженную на MI. В результате получим матрицу, у которой все элементы Q-го столбца за исключением Apq, равны 0. Отбрасывая этот столбец и главную строку, получим новую матрицу M1 с числом строк и столбцов на 1 меньше.

Над матрицей М1 повторяем те же операции, после чего получим матрицу M2 и т. д. Таким образом продолжаем до тех пор, пока не получим матрицу, содержащую одну строку из двух элементов, которую тоже считаем главной.

Затем объединим все главные строки, начиная с последней. После некоторой перестановки они образуют треугольную матрицу, эквивалентную исходной. На этом заканчивается этап вычислений, называемый Прямым ходом. Решив систему с полученной треугольной матрицей коэффициентов, найдём последовательно значения неизвестных XI (I = 1, 2, ..., N). На этом заканчивается Обратный ход.

Смысл выбора главного элемента состоит в том, чтобы сделать возможно меньшими числа MI и тем самым уменьшить погрешность вычислений.

Пример 3.4. Рассмотрим СЛАУ, состоящую из трех уравнений. Запишем расширенную матрицу

M2 = -1/6; M3 = -2/3.

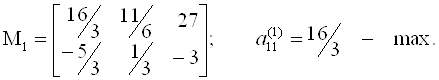
M2 = -5/16.

M2 = [ 87/96 174/32].

X3 = 6; X1 = 3; X2 = -2.

< Предыдущая		Следующая >