3.2. Метод Гаусса
Наиболее распространенным методом решения СЛАУ является метод Гаусса, в основе которого лежит идея последовательного исключения неизвестных. Существуют различные схемы, реализующие данный метод. Рассмотрим одну из них – Схему единственного деления.
Для простоты ограничимся рассмотрением СЛАУ с четырьмя неизвестными:
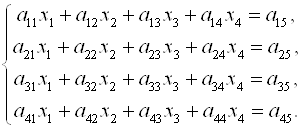 (3.7)
(3.7)
Пусть A11 ¹ 0 (ведущий элемент). Разделив первое уравнение на A11, получим Первую главную строку:
![]() (3.8)
(3.8)
Где ![]() (J = 2,3,4,5).
(J = 2,3,4,5).
Используя уравнение (3.8), можно исключить неизвестные X1 из 2-го,
3-го и 4-го уравнений системы (3.7). Для этого последовательно умножаем уравнение (3.8) на A21; A31; A41 и вычитаем результат из 2-го, 3-го и 4-го уравнений системы (3.7) соответственно.
В результате получим систему из трех уравнений:
![]()
 (3.9)
(3.9)
Где коэффициенты ![]() вычисляются по формуле
вычисляются по формуле
![]() (I = 2, 3, 4; J = 2, 3, 4, 5). (3.10)
(I = 2, 3, 4; J = 2, 3, 4, 5). (3.10)
Далее первое уравнение системы (3.9) делим на Ведущий элемент ![]() и получаем
и получаем
![]() (3.11)
(3.11)
Где ![]() , (J = 3, 4, 5).
, (J = 3, 4, 5).
Аналогично предыдущему шагу, исключая X2, как и X1, получим систему
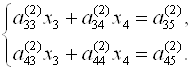 (3.12)
(3.12)
Здесь ![]() (I = 3, 4; j = 3, 4, 5).
(I = 3, 4; j = 3, 4, 5).
Разделив первое уравнение системы (3.12) на ![]() , получим:
, получим:
![]() (3.13)
(3.13)
Где ![]() (J = 4, 5).
(J = 4, 5).
Теперь с помощью уравнения (3.13) исключим X3 из второго уравнения системы (3.12), окончательно получим:
![]() , (3.14)
, (3.14)
Где ![]() (J=4, 5).
(J=4, 5).
Таким образом, исходную систему (3.7) привели к составленной из Главных строк (3.8), (3.11), (3.13) и (3.14) эквивалентной системе с треугольной матрицей(3.15):
![]()
 (3.15)
(3.15)
Из (3.15) последовательно находим
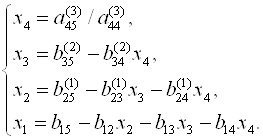 (3.16)
(3.16)
Итак, решение СЛАУ (3.7) распадается на два этапа:
· прямой ход (приведение системы (3.7) к треугольному виду (3.15));
· обратный ход (определение неизвестных по формуле (3.16)).
Пример 3.3.

Прямой ход:

Из выражений (3.10) вычислим коэффициенты ![]() :
:

Аналогично вычислим коэффициенты ![]() при (I = 3, 4) и составим систему
при (I = 3, 4) и составим систему
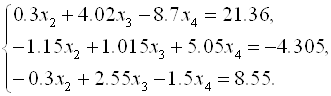
Разделив первое уравнение системы на ![]() , получим
, получим
![]()
Значит, ![]()
Из (3.12) вычислим ![]() Для I = 3 и J = 3, 4, 5:
Для I = 3 и J = 3, 4, 5:

Аналогично, вычислив коэффициенты для I = 4, получим:
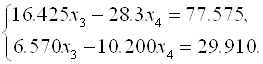
Разделив первое уравнение на a(2)33 = 16.425, получим:
![]()
Где ![]()
По формуле (3.14) находим коэффициенты ![]() :
:
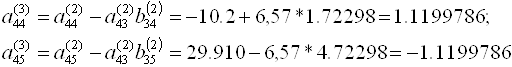
И записываем одно уравнение с одним неизвестным:
1.1199786X4 = -1.1199768.
X1 + 0.5X2 - 0.05X3 + 0.5X4 = 1.35;
X2 + 13.4X3 - 29X4 = 71.2;
X3 - 1.72298X4 = 4.72298;
1.11998X4 = -1.11998.
На этом закончен прямой ход.
Обратный ход:
X4 = -1.000;
X3 = 4.72298 - 1.72298 = 3;
X2 = 71.2 - 13.4 * 3-29 = 2;
X1 = 1.35 - 0.5 * 2 + 0.05 * 3 + 0.5 = 1.
| < Предыдущая | Следующая > |
|---|