3.1. Численное решение СЛАУ. Решение задач линейной алгебры
Линейные системы имеют в вычислениях очень большое значение, так как к ним может быть приведено приближенное решение широкого круга задач. Так, основными источниками возникновения СЛАУ являются теория электрических цепей, уравнения балансов и сохранения в механике, гидравлике и т. п.
Пусть дана система N линейных алгебраических уравнений с N неизвестными:
 (3.1)
(3.1)
Или в матричной форме:
![]() ; (3.2)
; (3.2)
Где
 (3.3)
(3.3)
- матрица коэффициентов системы (3.1);
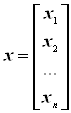 - вектор неизвестных;
- вектор неизвестных;  - вектор свободных членов.
- вектор свободных членов.
Если матрица A неособенная, т. е.
 (3.4)
(3.4)
То система (3.1) или эквивалентное ей матричное уравнение (3.2) имеют единственное решение. Действительно, при условии, что detA ¹ 0, существует обратная матрица A-1. Умножая обе части уравнения (3.2) слева на A-1, получим:
![]() (3.5)
(3.5)
Формула (3.5) даёт решение уравнения (3.2), причём единственное.
Пример 3.1.
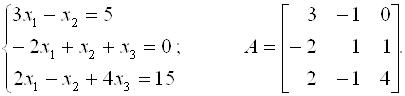
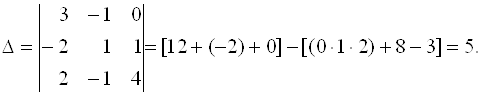
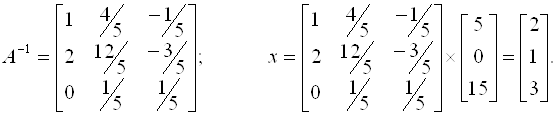
Для матрицы A порядка N > 4 непосредственное нахождение обратной матрицы A-1 требует много времени (операций). Поэтому формула (3.5) на практике употребляется достаточно редко.
Обычно значения неизвестных Xi (I = 1,2, ... N) могут быть получены по известным формулам Крамера:
![]() (3.6)
(3.6)
Здесь матрица Ai получается из матрицы A заменой её I-го столбца столбцом свободных членов.
Пример 3.2. Решим вышеприведенную систему по формулам Крамера:
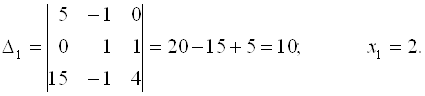

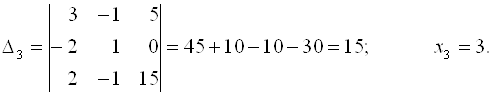
Применяемые в настоящее время методы решения СЛАУ можно разбить на две группы: Точные и приближённые.
Точными методами называются такие методы, которые в предположении, что вычисления ведутся точно (без округлений), за конечное число действий позволяют получить точные значения неизвестных Xi.
Приближенными методами называются такие методы, которые даже в предположении, что вычисления ведутся без округлений, позволяют получить решение системы (X1, X2, ..., Xn) лишь с заданной точностью. Точное решение СЛАУ в этих случаях может быть получено теоретически как результат бесконечного процесса.
К приближенным методам относятся метод простой итерации, метод Зейделя и т. п.
| < Предыдущая | Следующая > |
|---|