2.5. Вычисление определенных интегралов методами. Монте–Карло
Рассматриваемые ранее методы называются Детерминированными, то есть лишенными элемента случайности.
Методы Монте–Карло (ММК) – это численные методы решения математических задач с помощью моделирования случайных величин. ММК позволяют успешно решать математические задачи, обусловленные вероятностными процессами. Более того, при решении задач, не связанных с какими-либо вероятностями, можно искусственно придумать вероятностную модель (и даже не одну), позволяющую решать эти задачи. Рассмотрим вычисление определенного интеграла
 (2.20)
(2.20)
При вычислении этого интеграла по формуле прямоугольников интервал [A, B] разбиваем на N одинаковых интервалов, в серединах которых вычислялись значения подынтегральной функции. Вычисляя значения функции в случайных узлах, можно получить более точный результат:
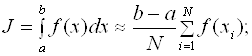 (2.21)
(2.21)
![]() (2.22)
(2.22)
Здесь γi - случайное число, равномерно распределенное на интервале
[0, 1]. Погрешность вычисления интеграла ММК ~ ![]() , что значительно больше, чем у ранее изученных детерминированных методов.
, что значительно больше, чем у ранее изученных детерминированных методов.
На рис. 2.5 представлена графическая реализация метода Монте-Карло вычисления однократного интеграла со случайными узлами (2.21) и (2.22).
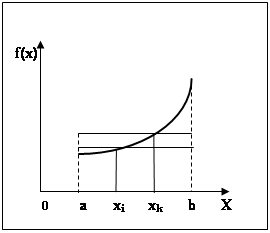 |
Рис. 2.5. Интегрирование методом Монте-Карло (1-й случай)
Однако при вычислении кратных интегралов детерминированными методами оценка погрешности перерастает в задачу порой более сложную, чем вычисление интеграла. В то же время погрешность вычисления кратных интегралов ММК слабо зависит от кратности и легко вычисляется в каждом конкретном случае практически без дополнительных затрат.
Рассмотрим еще один метод Монте-Карло на примере вычисления однократного интеграла:
 |
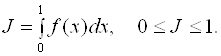 (2.23)
(2.23)
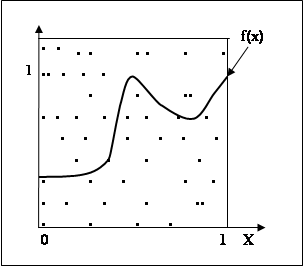
Рис. 2.6. Интегрирование методом Монте-Карло (2-й случай)
Как видно на рис. 2.6, интегральная кривая лежит в единичном квадрате, и если мы сумеем получать пары случайных чисел, равномерно распределенных на интервале [0, 1], то полученные значения (γ1, γ2) можно интерпретировать как координаты точки в единичном квадрате. Тогда, если этих пар чисел получено достаточно много, можно приблизительно считать, что
![]() . Здесь S – число пар точек, попавших под кривую, а N – общее число пар чисел.
. Здесь S – число пар точек, попавших под кривую, а N – общее число пар чисел.
Пример 2.1. Вычислить следующий интеграл:
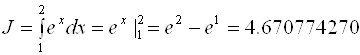
Поставленная задача была решена различными методами. Полученные результаты сведены в табл. 2.1.
Таблица 2.1
|
Число интервалов (точек) |
Метод левых прямоугольников |
Метод средних прямоугольников |
Метод правых прямоугольников |
Метод |
Метод Симпсона |
Метод |
|
10 |
4.44112722 |
4.66882868 |
4.90820465 |
4.25683746 |
4.67077443 |
4.62289422 |
|
100 |
4.64745932 |
4.67075481 |
4.69416706 |
4.62903035 |
4.67077427 |
4.69812790 |
Замечание. Выбор табличного интеграла позволил нам сравнить погрешность каждого метода и выяснить влияние числа разбиений на точность вычислений.
Вопросы для самопроверки
· Сформулируйте задачу численного интегрирования.
· Метод средних, левых и правых прямоугольников. Что можно сказать об их погрешности, трудоемкости?
· Задача численного интегрирования решена методом трапеций. Предложите и обоснуйте пути повышения точности (уменьшения погрешности) расчетов.
· Сравните метод трапеций и метод Симпсона.
· Какие методы Монте–Карло численного интегрирования вы знаете? Сравните эти методы с любым детерминированным.
· Необходимо вычислить интеграл методами трапеций, Симпсона и ММК, разбив область интегрирования на 77 интервалов (точек). Что можно сказать о точности и применимости этих методов?
| < Предыдущая | Следующая > |
|---|