2.4. Формула Симпсона
В этом методе предлагается подынтегральную функцию на частичном отрезке аппроксимировать параболой, проходящей через точки
(Xj, F(Xj)), где J = I-1; I-0.5; I, то есть подынтегральную функцию аппроксимируем интерполяционным многочленом Лагранжа второй степени:
![]()
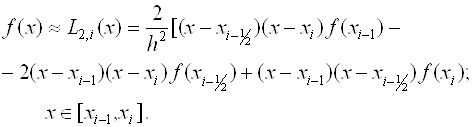 (2.14)
(2.14)
Проведя интегрирование, получим:

![]() (2.15)
(2.15)
Это и есть Формула Симпсона или формула парабол. На отрезке
[A, B] формула Симпсона примет вид
![]()
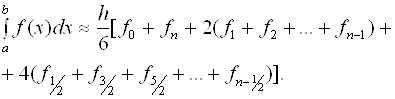 (2.16)
(2.16)
Графическое представление метода Симпсона показано на рис. 2.4.
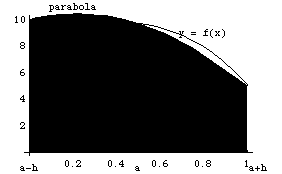
Рис. 2.4. Метод Симпсона
Избавимся в выражении (2.16) от дробных индексов, переобозначив переменные:
 (2.17)
(2.17)
Тогда формула Симпсона примет вид
 (2.18)
(2.18)
Погрешность формулы (2.18) оценивается следующим выражением:
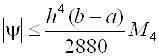 , (2.19)
, (2.19)
Где H·N = B - A, ![]() . Таким образом, погрешность формулы Симпсона пропорциональна O(H4).
. Таким образом, погрешность формулы Симпсона пропорциональна O(H4).
Замечание. Следует отметить, что в формуле Симпсона отрезок интегрирования обязательно разбивается на Четное число интервалов.
| < Предыдущая | Следующая > |
|---|