2.3. Формула трапеций
Если на частичном отрезке подынтегральную функцию заменить полиномом Лагранжа первой степени, то есть
![]()
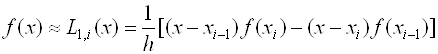 , (2.10)
, (2.10)
Тогда искомый интеграл запишется следующим образом:
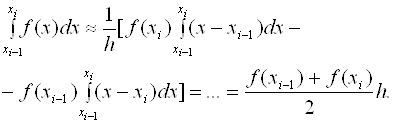 (2.11)
(2.11)
После подстановки выражения (2.11) в (2.5) составная формула трапеций примет вид
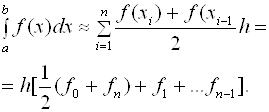 (2.12)
(2.12)
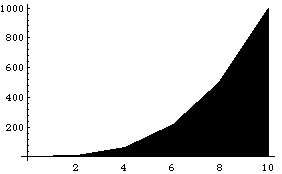
Графически метод трапеций представлен на рис. 2.3.
Рис. 2.3. Метод трапеций
Погрешность формулы (2.12) определяется выражением:
 (2.13)
(2.13)
Таким образом, погрешность метода трапеций Ψ ~ O(H²), но она в два раза больше, чем для формулы средних прямоугольников.
| < Предыдущая | Следующая > |
|---|