2.2. Формула прямоугольников

На частичном отрезке [Xi-1, Xi] заменим подынтегральную функцию полиномом Лагранжа нулевого порядка, построенным в одной точке. Естественно в качестве этой точки выбрать среднюю: Xi-0.5 = Xi - 0.5H. Тогда получим формулу

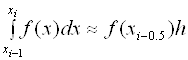. (2.6)

Подставив (2.6) в (2.5), получим составную формулу средних прямоугольников:

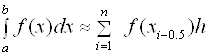. (2.7)

Графическая иллюстрация метода средних прямоугольников представлена на рис. 2.1.

Рис. 2.1. Интегрирование методом средних прямоугольников

Погрешность формулы (2.7) определяется выражением

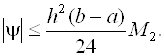(2.8)

Здесь . Таким образом, погрешность формулы (2.7) пропорциональна O(H2).

Замечание. Формулу (2.7) можно представить в ином виде:

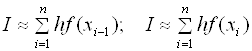. (2.9)

Эти формулы в выражении (2.9) называются формулой левых и правых прямоугольников соответственно. Графически метод левых и правых прямоугольников представлен на рис. 2.2.

А) б)

Рис. 2.2. Метод левых (а) и правых (б) прямоугольников

Однако из-за нарушения симметрии в формулах (2.9) их погрешность значительно больше, чем в методе средних прямоугольников и ~O(H).

< Предыдущая		Следующая >