2.1. Численное интегрирование. Постановка задачи

Задача численного интегрирования функции заключается в вычислении определенного интеграла на основании ряда значений подынтегральной функции. Численное вычисление однократного интеграла называется Механической квадратурой.

Мы будем рассматривать способы приближенного вычисления определенных интегралов

, (2.1)

Основанные на замене интеграла конечной суммой:

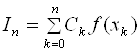, (2.2)

Где СK- числовые коэффициенты, а Xk Î [A, B], K = 0, 1, …, N.

Приближенное равенство

(2.3)

Называется квадратурной формулой, а XK – узлами квадратурной формулы. Погрешность квадратурной формулы определяется соотношением

. (2.4)

В общем случае погрешность квадратурной формулы (2.4) зависит как от выбора коэффициентов Ск , так и от расположения узлов Хк. Введем на отрезке [A, B] равномерную сетку с шагом H, тогда Xi = A + Ih, где (I = 0, 1, ..., N;
H·N = B-A). Теперь выражение (2.1) можно представить в виде суммы интегралов по частичным отрезкам:

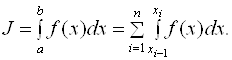(2.5)

Таким образом, для построения формулы численного интегрирования на отрезке [A, B] достаточно построить квадратурную формулу на частичном отрезке [Xi-1, Xi] и воспользоваться формулой (2.5).

< Предыдущая		Следующая >