1. Элементы теории погрешностей

Численное решение любой задачи, как правило, осуществляется приближенно, с различной точностью. Это может быть обусловлено неточностью исходных данных, конечной разрядностью вычислений (вручную или на ЭВМ) и т. п.

Главная задача численных методов – фактическое нахождение решения с требуемой или, по крайней мере, оцениваемой точностью.

Отклонение истинного решения от приближенного называется погрешностью. Полная погрешность вычислений состоит из двух составляющих:
1) неустранимая погрешность; 2) устранимая погрешность.

Неустранимая погрешность обусловлена неточностью исходных данных и никаким образом не может быть уменьшена в процессе вычислений.

Устранимая погрешность состоит из двух составляющих: а) погрешность аппроксимации (метода); б) погрешность вычислений. Эти составляющие могут быть уменьшены выбором более точных методов и увеличением разрядности вычислений.

Как правило, в дальнейшем нас будут интересовать корректно поставленные задачи вычисления.

Задача вычисления Y = A(X) Называется корректно поставленной, если для любых входных данных из некоторого класса решение задачи существует, единственно и устойчиво по входным данным (т. е. непрерывно зависит от входных данных задачи).

В сформулированном понятии Корректности учтены достаточно естественные требования, т. к. чтобы численно решать задачу, нужно быть уверенным, что ее решение Существует. Столь же естественны требования Единственности и Устойчивости решения.

Рассмотрим подробнее понятие Устойчивости. Обычно нас интересует решение Y, Соответствующее входным данным X. Реально мы имеем возмущенные входные данные с погрешностью δX, т. е. X + δX, и находим возмущенное решение:

Y + δY = A(X+δX).

Эта погрешность входных данных порождает Неустранимую погрешность решения:

δY = A(x+δX) - A(X).

Если решение непрерывно зависит от входных данных, то всегда при , И задача устойчива по входным данным. Здесь символ
|| || - Норма.

Если X – точное значение величины, а X* – Приближенное значение, то Абсолютная погрешность приближения определяется выражением
.

Относительной погрешностью величины называется отношение абсолютной погрешности к модулю ее точного значения: δ = Δ / |X|.

Достаточно часто точное значение величины неизвестно, поэтому указывают границы погрешности:

(1.1)

(1.2)

Рассмотрим подробнее погрешность округления чисел, участвующих в вычислениях. В позиционной системе счисления с основанием R Запись

(1.3)

Означает, что

Здесь R – целое число, большее единицы. Каждое из чисел может принимать одно из значений {0, 1, …, r-1}. Числа называются Разрядами, Например: – третий разряд перед запятой, – второй разряд после запятой.

Запись вещественного числа в виде (1.3) называется также его представлением в форме Числа с фиксированной запятой. В ЭВМ чаще всего используется представление Чисел в форме с плавающей запятой. Так как наиболее часто в компьютерах применяется двоичная система с плавающей запятой, то вещественное число можно представить виде

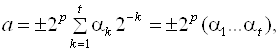(1.4)

Где

Здесь P - целое число называется порядком числа A, а – мантиссой.

Если исходная величина или промежуточный результат требуют большего числа разрядов, то производится округление до T – го разряда. Значащие цифры называются верными до T – го разряда, если абсолютная величина разности между A* и A меньше или равна половине единицы младшего разряда:

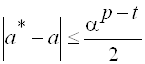. (1.5)

Ограничения на порядки чисел, представляемых в ЭВМ , порой приводят к прекращению вычислений (так называемое исчезновение порядка); в других случаях относительно небольшая разрядность представления чисел в ЭВМ приводит к недопустимому искажению результата вычислительной погрешностью.

Приведем несколько примеров иллюстрирующих это и способы (приемы) уменьшения вычислительной погрешности за счет несложных алгебраических преобразований.

Рассмотрим типичный пример, в котором порядок выполнения операций существенно влияет на погрешность результата.

Пример 1.1. Необходимо отыскать минимальный корень уравнения. Вычисления производим в десятичной системе счисления, причем в числе после округления оставляем четыре действующие цифры (разряда):

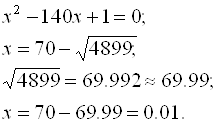
Рассмотрим другой алгоритм вычисления корня, для чего избавимся от иррациональности в числителе:

Как видно из сравнения полученных результатов, применение "неудачного" алгоритма завышает результат на 30 %. Это явление в прикладной математике (в практике вычислений) называется Потерей значащих цифр, и часто наблюдается при вычитании близких величин. Потеря значащих цифр, например, довольно часто приводит к существенному искажению результатов при решении даже сравнительно небольших систем линейных алгебраических уравнений.

Пример 1.2. На машине с плавающей запятой необходимо вычислить значение суммы

Эту сумму можно вычислить двумя способами:

Оказывается, для второго алгоритма вычислительная погрешность будет существенно меньше.

Тестовые расчеты на конкретной ЭВМ по первому и второму алгоритмам показали, что величина погрешности для обоих алгоритмов составляет 2∙10-4 и 6∙10-8соответственно. Причина этого ясна, если вспомним, как числа представлены в ЭВМ (см. рис. 1.1).

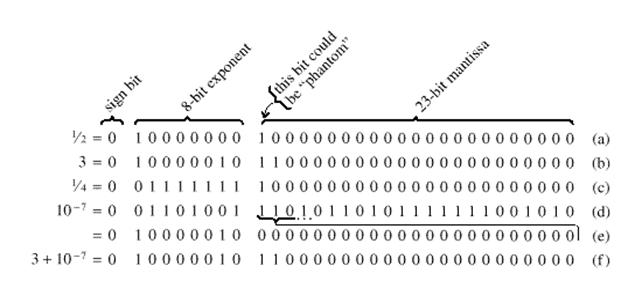
Рис. 1.1. Представление чисел с плавающей точкой в типичном
32-бит (4 - байт) формате:

А) Число ½; B) Число 3; C) число ¼; D) Число 10-7, представленное в машине с максимальной точностью (нормализованное); E) То же самое число 10-7, но представленное с тем же порядком, что и число 3*; F) Сумма чисел 3 + 10-7, которая эквивалентна 3.

Этот пример ярко иллюстрирует тот факт, что даже если оба слагаемых представлены в компьютере точно, то их сумма может быть представлена с погрешностью, особенно если слагаемые различаются на порядки.

При оценке погрешностей арифметических действий следует учитывать следующее:

А) абсолютная погрешность алгебраической суммы

не превышает суммы абсолютных погрешностей ее членов: