8. Угол между двумя прямыми

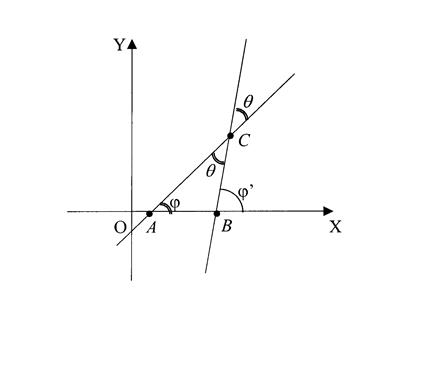
Рассмотрим две прямые (не параллельные оси ), заданные их уравнениями с угловыми коэффициентами (рис.8).

, где (1)

, где (2)

Рис.8

Требуется определить угол между ними, где за угол будем принимать наименьший угол, отсчитываемый против хода часовой стрелки, на который вторая прямая повернута относительно первой (). Угол (см. рис.8) есть угол треугольника . Известно, что внешний угол треугольника равен сумме внутренних, с ним не смежных. Поэтому

или ;

Отсюда на основании формулы

Заменяя и соответственно на и , будем иметь

(3)

Введем теперь условия параллельности и перпендикулярности двух прямых.

А) Если прямые (1) и (2) параллельны, то и, следовательно,

. (4)

Правило 1. Прямые на плоскости параллельны тогда и только тогда, когда их угловые коэффициенты равны между собой.

Б) Если прямые перпендикулярны, то и, следовательно,

Отсюда

и . (5)

Правило 2. Две прямые на плоскости перпендикулярны тогда и только тогда, когда их угловые коэффициенты обратны по величине и противоположны по знаку.

Пусть теперь уравнения прямых заданы в общем виде:

(6)

. (7)

Предполагая, что и , получаем

(8)

. (9)

Следовательно, угловые коэффициенты этих прямых есть

. (10)

Подставляя в формулу (3) значения и найдем угол между прямыми

. (11)

Отсюда получаем:

1) условие параллельности прямых ()

, (12)

2) условие перпендикулярности прямых ()

. (13)

Пример. Найти угол между прямыми

Решение. Воспользуемся формулой (3). Так как уравнения прямых заданы в общем виде, где то

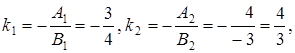
Тогда

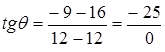
И так как деление невозможно, то не существует. Следовательно, , т. е. прямые перпендикулярны. Можно было составить выражение , оно равно нулю.

< Предыдущая		Следующая >