7. Уравнение прямой с угловым коэффициентом
Если в общем уравнении прямой ![]() , то разделив все его члены на
, то разделив все его члены на ![]() , получим уравнение вида:
, получим уравнение вида:
![]() или
или ![]() (1)
(1)
|
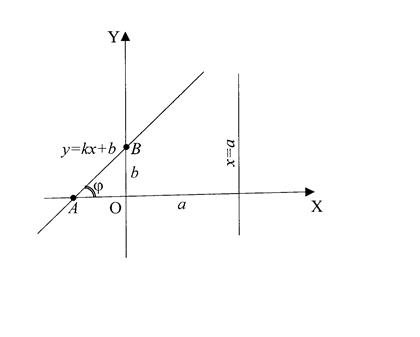 Обозначим
Обозначим | < Предыдущая | Следующая > |
|---|
Если в общем уравнении прямой ![]() , то разделив все его члены на
, то разделив все его члены на ![]() , получим уравнение вида:
, получим уравнение вида:
![]() или
или ![]() (1)
(1)
|
 Обозначим
Обозначим | < Предыдущая | Следующая > |
|---|