9. Уравнение прямой, проходящей через данную точку в данном направлении
 Пусть прямая
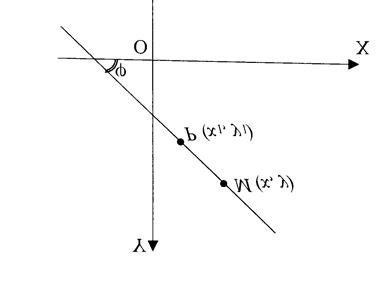
Пусть прямая ![]() образует угол
образует угол ![]() с положительным направлением
с положительным направлением ![]() (рис.9) и проходит через данную точку
(рис.9) и проходит через данную точку ![]() . Выведем уравнение этой прямой, предполагая сначала, что прямая не параллельна оси
. Выведем уравнение этой прямой, предполагая сначала, что прямая не параллельна оси ![]() . В этом случае уравнение имеет вид
. В этом случае уравнение имеет вид ![]() , (1)
, (1)
|
![]() . (2)
. (2)
Вычитая из равенства (1) равенство (2), получим
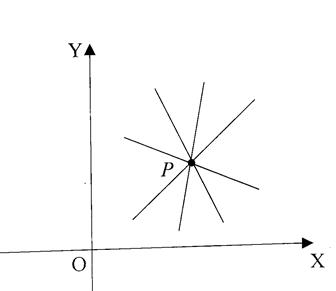
![]() (3)
(3)
Это и есть уравнение искомой прямой. Если ![]() - заданное число, то уравнение (3) представляет вполне определенную прямую.
- заданное число, то уравнение (3) представляет вполне определенную прямую.
|
|
Решение. Разрешив уравнение гипотенузы относительно ![]() , найдем ее угловой коэффициент:
, найдем ее угловой коэффициент: ![]() Катеты равнобедренного прямоугольного треугольника наклонены к гипотенузе под углом
Катеты равнобедренного прямоугольного треугольника наклонены к гипотенузе под углом ![]() . Подставляя в формулу
. Подставляя в формулу  значение
значение ![]() И
И ![]() , получим уравнение для определения угловых коэффициентов катетов
, получим уравнение для определения угловых коэффициентов катетов
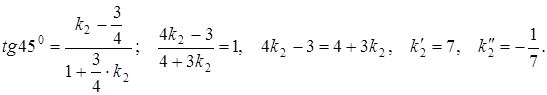
Зная точку ![]() на катетах, получим их уравнения
на катетах, получим их уравнения
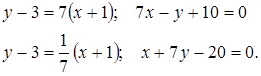
| < Предыдущая |
|---|