4. Деление отрезка в данном отношении

Предположим, что отрезок (рис.5), соединяющий точки и разделен точкой на два отрезка и , причем отношение к равно:

. (1)

Рис.5

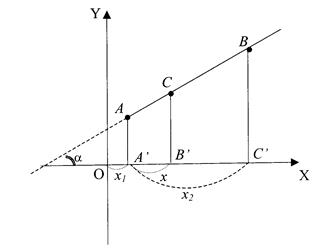Требуется выразить координаты 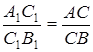и точки через координаты концов отрезка . Опустим перпендикуляры И , соответственно из точек и на ось . Тогда получим, что три параллельные прямые , пересекают стороны угла, образованного прямыми и . Как известно, пучок параллельных прямых рассекает стороны угла на пропорциональные части, поэтому , откуда на основании равенства (1) будем иметь:

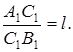(2)

Из рисунка 5 видно, что

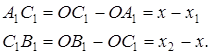
Подставляя эти выражения в формулу (2), получим

. (3)

Решая уравнение (3) относительно неизвестной , будем иметь

Аналогично,

Итак, координаты точки , делящей отрезок в отношении (считая от к ), определяются формулами

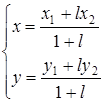. (4)

Если точка делит отрезок Пополам, то и, следовательно, и тогда

(5)

< Предыдущая		Следующая >