5. Площадь треугольника

Рис.6

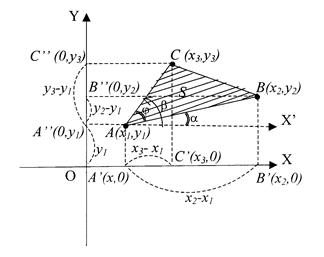Пусть требуется найти площадь треугольника (рис.6) с вершинами

Пусть а углы, образованные этими сторонами с осью , соответственно равны и .

Имеем

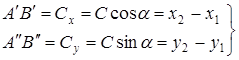(1)

.

(2)

Пусть (рис.6), тогда По формуле получим

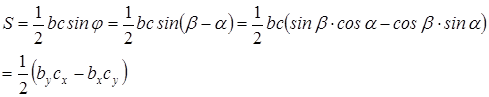(3)

Отсюда в силу (1) и (2) имеем

. (4)

Используя понятие определителя второго порядка , формулу (4) можно записать в удобной форме

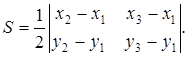(5)

Если точки находятся на одной прямой, то площадь .

Замечание. Определение площади многоугольника сводится к определению площадей треугольников. Для этого достаточно разбить многоугольник на треугольники, площади которых вычисляются по формуле (4).

Пример 1. Точки И - три вершины параллелограмма, причем и - противоположные вершины. Найти четвертую вершину.

Решение. Диагонали парал­лелограмма в точке пересе­чения делятся пополам, по­этому координаты точки - пересечения диагоналей найдем как координаты се­редины отрезка . Обозна­чим их через и , полу­чим, что

. Зная координаты точки - середины диаго­нали и координаты од­ного из ее концов , по формулам имея а ко­ординаты искомой точки , тогда

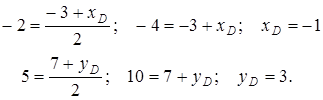
Итак, искомая вершина имеет координаты

Пример 2. Найти площадь треугольника, вершины которого находятся в точках

Решение. Для решения задачи воспользуемся формулой

.

Возьмем Подставим эти числа в формулу

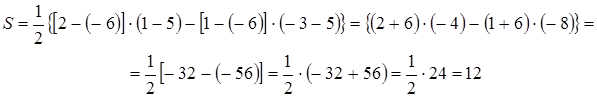
кв. ед.

< Предыдущая		Следующая >