34. Метод параллельных сечений

Если задано уравнение той или иной поверхности, то возникает задача исследования ее формы и расположения относительно координатных осей.

Для решения этой задачи обычно применяют метод параллельных сечений, который состоит в том, что поверхность пересекается несколькими плоскостями, параллельными плоскостям координат. Форма и размеры полученных сечений позволяют выяснить форму самой поверхности.

Рассмотрим этот метод на примерах.

Пример 1. Исследовать сечения эллипсоида 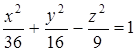плоскостями

Решение. Рассмотрим сначала сечение эллипсоида плоскостями , где

Подставляя в уравнение эллипсоида, получим

или ,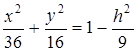

Отсюда

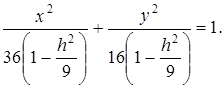
Обозначив 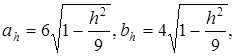получим в сечении эллипс

С полуосями .

При получаем:

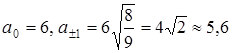
Таким образом наибольший эллипс получается в сечении плоскости . Если поднимать или опускать эту плоскость вдоль оси Параллельно плоскости , то размеры сечений уменьшаются до тех пор, пока при не превратятся в точку . При дальнейшем увеличении плоскость эллипсоида пересекать уже не будет, так как корень, входящий в выражение для , станет мнимым.

В сечении плоскостями, параллельными , будут также получаться эллипсы. В частности, в сечении координатными плоскостями и получатся наибольшие по размерам эллипсы

и .

Проведенное исследование позволяет сделать вывод, что эллипсоид является овальной поверхностью (рис.32).

Пример 2. Исследовать форму и расположение относительно системы координат поверхности

Решение. Используем метод сечений. Положим в данном уравнении , получим

.

Отсюда следует, что должна быть величиной неотрицательной. Обозначая , получим в сечении плоскостью линию

Эта линия является окружностью радиуса с центром на оси . Следовательно, данная поверхность является поверхностью вращения вокруг оси . Чтобы выяснить, вращением какой линии она получается, пересечем поверхность плоскостью . В сечении получится парабола на плоскости : Вершина ее лежит в точке , а направлена парабола в отрицательную сторону оси .

Рис.38

Таким образом, исследуемая поверхность является параболоидом вращения, расположение которого указано на рис.38.

Пример 3. Показать, что уравнение определяет однополостный гиперболоид вращения вокруг оси .

Решение. Рассмотрим сечение данной поверхности плоскостями , перпендикулярными оси . В сечении получим линию , где

Рис.39

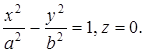Таким образом, в любом сечении, перпендикулярном оси , получается окружность радиуса R, т. е. данная поверхность есть поверхность вращения вокруг оси . Выясним, вращением какой линии получена эта поверхность. Пересечем поверхность какой-либо плоскостью, проходящей через поверхность вращения, например, плоскостью . В сечении получим линию Эта есть гипербола с полуосями . Вращаясь вокруг оси , она и образует данную поверхность, являющуюся поэтому однополостным гиперболоидом вращения вокруг оси (рис.39).

В случае, когда в уравнении отсутствуют члены с произведением координат , это уравнение приводится к каноническому виду выделением полных квадратов по И параллельным переносом осей координат.

Точки пересечения прямой с поверхностью второго порядка ищутся следующим образом: уравнение прямой приводится к параметрическому виду:

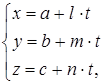
Затем значения подставляют в уравнение поверхности. Из полученного квадратного уравнения для находим значения параметра , отвечающие точкам пересечения. Если корни этого уравнения совпали, то прямая является касательной к поверхности, если корни мнимые – точек пересечения нет.

Пример 4. Какую поверхность определяет уравнение

?

Решение. Чтобы привести данное уравнение к каноническому виду, выделяем полные квадраты по :

Или

Сравнивая полученное уравнение с каноническими уравнениями, видим, что это есть уравнение однополостного гиперболоида, центр которого смещен в точку . Обозначим

И запишем уравнение

.

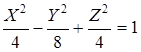Новые оси Параллельны старым. Относительно этих осей гиперболоид имеет вид, представленный на рис.39.

Пример 5. Найти точки пересечения эллипсоида с прямой при 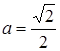. При каком значении прямая касается эллипсоида?

Решение. Запишем уравнение данной прямой в параметрическом виде

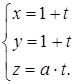
Подставив значения в уравнение эллипсоида

Получим квадратное уравнение для :

Из которого находим значения параметра , соответствующее точкам пересечения прямой с эллипсоидом:

При 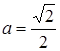получим два значения: .

Следовательно, точки пересечения следующие:

.

Если прямая касается эллипсоида, то должно быть , а это произойдет в том случае, если подкоренное выражение равно нулю. Следовательно, при =0, 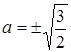. Т. е. при 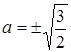прямая является касательной.

< Предыдущая		Следующая >