32. Цилиндрические поверхности

Поверхность, описываемая прямой, остающейся параллельной некоторой данной прямой И пересекающей данную линию , называется Цилиндрической поверхностью. Линия называется ее Направляющей, а каждое положение движущейся прямой – Образующей. Всегда можно выбрать систему координат так, чтобы прямая совпадала с одной из координатных осей. Уравнение цилиндрической поверхности (рис.28) с образующими, параллельными оси , не содержит , т. е. имеет вид

(1)

Уравнение цилиндрической поверхности, образующие которой параллельны оси или оси , имеют вид

(2)

Или соответственно

(3)

В качестве направляющей поверхности (1) можно взять ее линию пересечения с плоскостью . Уравнение этой направляющей

:

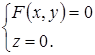
Аналогично, направляющими цилиндрических поверхностей (2) и (3) являются соответственно лини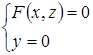и

: и :

Если уравнение (1) является алгебрагическим уравнением второй степени, то цилиндрическая поверхность называется Цилиндром второго порядка.

На рисунках 29,30,31 изображены эллиптический, гиперболический и параболические цилиндры, заданные своими каноническими уравнениями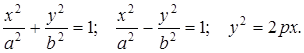

Возможен также случай, когда уравнение (1) распадается на два линейных множителя. В этом случае соответствующий цилиндр состоит из пары плоскостей, параллельных оси .

Пусть в пространстве задана линия как пересечение двух поверхностей

(4) Исключая координату , получим уравнение вида

которое определяет цилиндрическую поверхность, проектирующую линию на плоскость . Аналогично, чтобы получить уравнение цилиндра, проектирующего линию на плоскость (или ), надо из уравнений (4) исключить координату (или ).

Пример 1. Какую поверхность определяет уравнение

Решение. Так как данное уравнение не содержит , то рассматриваемая поверхность является цилиндром с образующими, параллельными оси . Направляющая этого цилиндра

или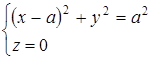

Является окружностью с центром на оси в точке и радиусом . Таким образом данное уравнение определяет круговой цилиндр, ось которого идет по прямой

Пример 2. Установить вид поверхности, заданной уравнением

Решение. Данное уравнение не содержит , поэтому рассматриваемая поверхность есть цилиндр с образующими, параллельными оси . Его направляющая есть

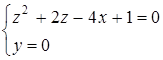
Из которых ясно, что направляющая есть парабола на плоскости с вершиной в точке , направленная в положительную сторону оси . Таким образом, рассматриваемая поверхность является параболическим цилиндром.

Пример 3. Какую поверхность определяет уравнение

?

Решение. Выделим полные квадраты из данного уравнения по и :

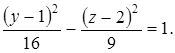
Данная поверхность есть гиперболический цилиндр с образующими, параллельными оси , так как данное уравнение не содержит , а направляющая цилиндра есть гипербола

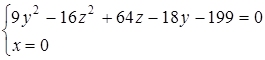или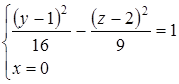

С центром в точке и действительной осью, параллельной оси .

Пример 4. Какую поверхность определяет уравнение ?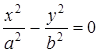

Решение. Левая часть данного уравнения распадается на произведение двух линейных множителей

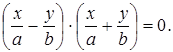
Следовательно, оно определяет пару плоскостей

или ,

Пересекающихся по оси .

< Предыдущая		Следующая >