31. Плоскость, проходящая через прямую и точку

Пусть даны точка и прямая, заданная уравнением

Рис.27

. Требуется найти уравнение проходящей через них плоскости. (Точка не лежит на данной прямой). Из уравнения данной прямой находим координаты точки .

Пусть - произвольная точка плоскости . При любом ее выборе направляющий вектор прямой и векторы

и

лежат в одной плоскости и поэтому их смешанное произведение равно нулю:

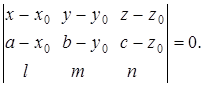
Раскрывая определитель, получим уравнение искомой плоскости.

Совершенно так же найдем уравнение плоскости, проходящей через две параллельные или пересекающиеся прямые: на одной из них берется любая точка (не лежащая на другой прямой), и плоскость проводится через вторую прямую и точку .

Пример. Провести плоскость через прямую и точку .

Решение. Убедимся, что точка не лежит на прямой, данной в условии

Из уравнения данной прямой следует, что точка лежит на этой прямой. Пусть - произвольная точка искомой плоскости, тогда векторы , и компланарны. Следовательно,

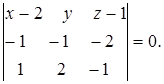
Раскроем определитель:

Таким образом искомая плоскость имеет уравнение

< Предыдущая		Следующая >