30. Взаимное расположение прямых и плоскостей в пространстве

Случай 1. Прямая и плоскость пересекаются под углом . Определим угол .

(1)

(2)

Направляющий вектор данной прямой есть вектор Нормальный вектор данной плоскости есть вектор . Угол - угол между пря­мой и плоскостью .

Обозначим через угол между векторами и , тогда

если - острый угол (3)

И

если - тупой угол. (4)

В первом случае (3)

Во втором случае (4)

. (6)

Так как положительно в обоих случаях

Так как

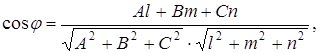(7)

То

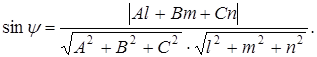(8)

По этой формуле определяется синус искомого угла, а затем и сам угол.

Пример. Найти угол между прямой

Решение. Вычислим коэффициенты направляющего вектора данной пря­мой :

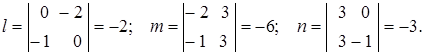(4)

Координаты нормального вектора данной плоскости (3) есть числа

(5)

Т. е. .

Подставляя значения (4) - (5) в формулу

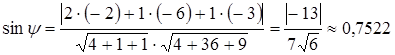
Случай 2. Прямая и плоскость параллельны в том и только в том случае, когда направляющий вектор данной прямой перпендикулярен к нормальному вектору данной плоскости , тогда скалярное произ­ведение векторов равно нулю, т. е.

Полученное равенство есть Условие параллельности прямой и плоскости.

Случай 3. Прямая и плоскость перпендикулярны.

;

Прямая перпендикулярна к плоскости в том и только в том слу­чае, когда направляющий вектор данной прямой коллинеарен нор­мальному вектору данной плоскости , т. е. соответственные координаты этих векторов должны быть пропорциональны, т. е.

Это соотношение есть Условие перпендикулярности прямой и плоскости.

Пример 1. Найти точку пересечения прямой и плоско­сти

Решение. Приведем данное уравнение прямой к параметрическому виду

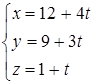
Подставим выражения для и в уравнение плоскости:

Откуда получим . Подставим значение в параметрическое уравнение прямой и получим координаты искомой точки пересечения прямой и плоско­сти

Искомая точка

Пример 2. Найти проекцию точки на плоскость

Решение. Вектор перпендикулярен к данной плоскости, и в то же время будет направляющим вектором перпендикуляра . Поэтому каноническое уравнение перпендикуляра будет иметь вид

Параметрическое уравнение прямой

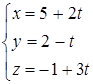
Подставляя значения , из полученных равенств в данное уравнение плоскости:

Найдем Значение отвечает точке , как точка пересечения прямой с данной плоскостью. Следовательно, координаты точки получим, подставив в параметрическое уравнение прямой :

Следовательно, координаты точки .

< Предыдущая		Следующая >