3. Расстояние между двумя точками на плоскости
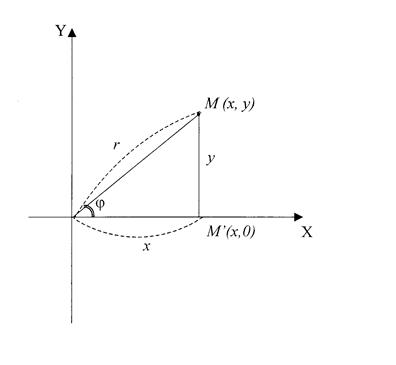
А) найдем сначала расстояние 
Точки 
от начала координат 
(рис.3).
Расстояние 
является гипотенузой прямоугольного 
с катетами
и 
. По теореме Пифагора
. (1)
Таким образом, расстояние точки от начала координат равно корню квадратному из суммы квадратов координат этой точки.
|
Б) в общем случае, пусть для точек 
И 
(рис.4) требуется найти расстояние 
между этими точками.
|
|
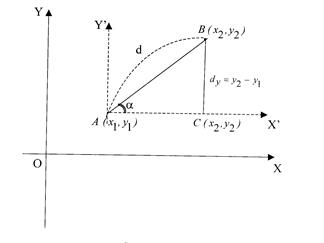Выберем новую систему координат 
Начало которой совпадает с точкой 
и оси которой параллельны с ними. Тогда в новой системе координат точки и 
будут иметь координаты 
и 
. Отсюда на основании формулы (1) получаем
, (2)
Т. е. расстояние между точками плоскости равно корню квадратному из суммы квадратов разностей одноименных координат этих точек.
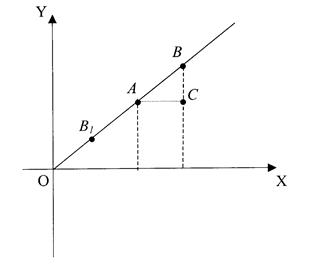Пример 1. Точки 
и 
лежат на биссектрисе первого координатного угла. Расстояние между ними равно 4 единицы масштаба. Найти координаты точки .
Решение. Так как точка лежит на биссектрисе первого координатного угла, то ее абсцисса и ордината между собой равны. В равнобедренном прямоугольном треугольнике 
гипотенуза 
, а 
. Тогда по теореме Пифагора
.
Таким образом абсцисса искомой точки (а значит, и ее ордината) получится из абсциссы точки , если к ней сначала прибавить, а потом из нее вычесть 
, и задача имеет два решения:
и 
.
Пример 2. Найти расстояние между точками 
и 
.
Решение. По формуле (2) для расстояния 
между двумя точками, если 
, получаем
Ед. масштаба.
| < Предыдущая | Следующая > |
|---|
